
【题目】如图,抛物线y=![]() 过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
(1)求抛物线的解析式,并写出顶点M的坐标;
(2)连接OC,CM,求tan∠OCM的值;
(3)若点P在抛物线的对称轴上,连接BP,CP,BM,当∠CPB=∠PMB时,求点P的坐标.

【答案】(1) ![]() ,(2,﹣1);(2)
,(2,﹣1);(2)![]() ;(3) (2,2+
;(3) (2,2+![]() )或(2,2﹣
)或(2,2﹣![]() ).
).
【解析】
试题分析:(1)根据待定系数法,可得函数解析式;根据顶点式解析式,可得顶点坐标;
(2)根据勾股定理及逆定理,可得∠OMC=90°,根据正切函数,可得答案;
(3)根据相似三角形的判定与性质,可得PM的值,可得M点坐标.
试题解析:(1)由抛物线y=![]() 过点C(4,3),得
过点C(4,3),得
![]() ,解得a=1,
,解得a=1,
抛物线的解析式为![]() ,顶点M的坐标为(2,﹣1);
,顶点M的坐标为(2,﹣1);
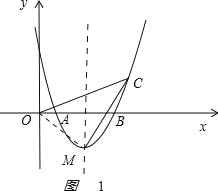
(2)如图1,
连接OM,![]() =
=![]() =25,
=25,![]() =
=![]() =5,
=5,![]() =
=![]() =20,
=20,
∴![]() +
+![]() =
=![]() ,
,
∴∠OMC=90°,OM=![]() ,CM=
,CM=![]() ,
,
tan∠OCM=![]() ;
;
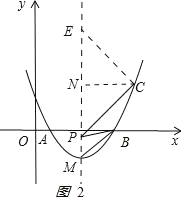
(3)如图2,
过C作CN⊥对称轴,垂足N在对称轴上,取一点E,使EN=CN=2,连接CE,EM=6.
当y=0时,![]() ,解得
,解得![]() =1,
=1,![]() =3,
=3,
∴A(1,0),B(3,0).
由CN=EN,PB=PM,得
∠CEP=∠PMB=∠CPB=45°.
∵∠CPM=∠CEP+∠ECP,
∴∠ECP=∠BPM,
∴△CEP∽△PMB,
∴![]() ,解得MB=
,解得MB=![]() ,CE=
,CE=![]() ,
,
∴![]() ,解得PM=
,解得PM=![]() ,
,
P点坐标为(2,2+![]() )或(2,2﹣
)或(2,2﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .

(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.请你仿照小森的思考方式,求出这个八边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的表示集合的大括号内: ![]() ,﹣0.
,﹣0. ![]() ,﹣(﹣2),﹣
,﹣(﹣2),﹣ ![]() ,1.732,
,1.732, ![]() ,0,
,0, ![]() ,1.1010010001…(每两个1之间依次多一个0) 整 数{…}
,1.1010010001…(每两个1之间依次多一个0) 整 数{…}
正分数{…}
无理数{…}
实 数 {…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,某中学以“每天阅读l小时”为主题,对学生最喜爱的书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)请把折线统计图(图1)补充完整;
(2)如果这所中学共有学生900名,那么请你估算最喜爱科普类书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(m,n)在y=![]() 的图象上,且m(n﹣1)≥0.
的图象上,且m(n﹣1)≥0.
(1)求m的取值范围;
(2)当m,n为正整数时,写出所有满足题意的A点坐标,并从中随机抽取一个点,求:在直线y=﹣x+6下方的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经统计,2016年除夕夜观看春晚直播的观众约达10.3亿人,用科学记数法表示10.3亿正确的是( )
A.1.03×109
B.1.03×1010
C.10.3×109
D.103×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学参加环保知识竞赛,将学生的成绩(得分取整数)进行整理后分成五组
绘成条形统计图如图所示,图中从左到右各小组小长方形的高的比是1:2:6:4:2,最右边一组的人数是6,结合图形提供的信息解答下列问题:
(1)该班共有多少名同学参赛?
(2)成绩落在哪组数据范围内的人数最多,
是多少?
(3)求成绩在60分以下(含60分)的人数是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com