
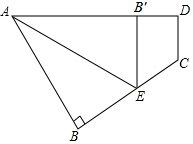
 如图所示,一个四边形纸片ABCD,∠B=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,且CD∥B′E.
如图所示,一个四边形纸片ABCD,∠B=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,且CD∥B′E.分析 (1)根据翻着的性质,可得∠B′,根据平行线的性质,可得∠D,根据垂线的定义,可得答案;
(2)根据平行线的性质,可得∠BEB,根据翻折的性质,可得∠AEB,根据直角三角形的性质,可得答案.
解答 解:(1)AD⊥BC,理由如下:
∵△AB′E是△ABE沿AE折叠得到的,
∴∠B′=∠B=90°.
∵CD∥B′E,
∴∠D=∠AB′E=90°,
∴AD⊥BC;
(2)∵CD∥B′E,
∴∠BEB′=∠C=122°,
∵△AB′E是△ABE沿AE折叠得到的,
∴∠AEB′=∠AEB=$\frac{1}{2}$∠BEB′=61°
∵∠B=90°.
∴∠EAB=90°-∠AEB=29°.
点评 本题考查了多边形的内角与外角,利用翻折的性质、平行线的性质是解题关键,又利用了直角三角形的性质.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:填空题
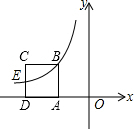 如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.
如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )
如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )| A. | 25°18′27″ | B. | 64°41′33″ | C. | 74°4133″ | D. | 64°41′43″ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
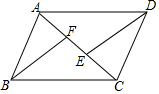 如图,在四边形ABCD中,AD∥BC,点E,F在对角线AC上,且AE=CF,∠ADE=∠CBF.不添加字母及辅助线,写出图中两对全等三角形,并选一对进行证明.
如图,在四边形ABCD中,AD∥BC,点E,F在对角线AC上,且AE=CF,∠ADE=∠CBF.不添加字母及辅助线,写出图中两对全等三角形,并选一对进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
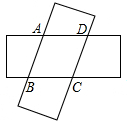 如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.
如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com