
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.
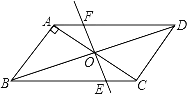
【答案】(1)证明见解析;(2)证明见解析;(3)四边形BEDF可以是菱形.理由见解析;AC绕点O顺时针旋转45°时,四边形BEDF为菱形.
【解析】试题分析:(1)当旋转角为90°时,∠AOF=90°,由AB⊥AC,可得AB∥EF,即可证明四边形ABEF为平行四边形;
(2)证明△AOF≌△COE即可;
(3)EF⊥BD时,四边形BEDF为菱形,可根据勾股定理求得AC=2,∴OA=1=AB,又AB⊥AC,∴∠AOB=45°.
试题解析:(1)证明:当∠AOF=90°时,
∵∠BAO=∠AOF=90°,
∴AB∥EF,
又∵AF∥BE,
∴四边形ABEF为平行四边形.
(2)证明:∵四边形ABCD为平行四边形,
在△AOF和△COE中
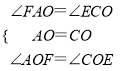 .
.
∴△AOF≌△COE(ASA).
∴AF=EC.
(3)解:四边形BEDF可以是菱形.
理由:如图,连接BF,DE
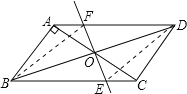
由(2)知△AOF≌△COE,得OE=OF,
∴EF与BD互相平分.
∴当EF⊥BD时,四边形BEDF为菱形.
在Rt△ABC中,AC=![]() =2,
=2,
∴OA=1=AB,
又∵AB⊥AC,
∴∠AOB=45°,
∴∠AOF=45°,
∴AC绕点O顺时针旋转45°时,四边形BEDF为菱形.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE相交于点F.则∠BFD的度数为( )

A. 45° B. 90° C. 60° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E,F分别是AC,BC的中点,直线EF与⊙O交于点G,H.若⊙O的半径为2,则GE+FH的最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计). 
(1)要使鸡场面积最大,鸡场的长度应为多少米?
(2)如果中间有n(n是大于1的整数)道篱笆墙,要使鸡场面积最大,鸡场的长应为多少米?比较(1)(2)的结果,要使鸡场面积最大,鸡场长度与中间隔离墙的道数有怎样的关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO中,AB⊥OB,OB= ![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( ) 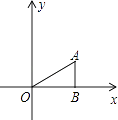
A.(﹣1, ![]() )
)
B.(﹣1, ![]() )或(﹣2,0)
)或(﹣2,0)
C.( ![]() ,﹣1)或(0,﹣2)
,﹣1)或(0,﹣2)
D.( ![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
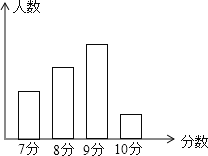
【题目】体育课上,体育老师对七年级一个班的学生进行了立定跳远项目的测试,得到一组测试分数的数据,并将测试所得分数绘制如图所示的统计图,图中从左到右的学生数人数之比为2 : 3 : 4 : 1,且成绩为8分的学生有12人,根据以上信息解答下列问题:
(1) 这个班级有多少名学生?
(2)这组数据的众数是 分,中位数是 分.
(3)这个班级学生立定跳远项目测试的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(0,﹣4)的抛物线y= ![]() x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
(1)求抛物线的解析式;
(2)将抛物线y= ![]() x2+bx+c向上平移
x2+bx+c向上平移 ![]() 个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)将x轴下方的抛物线图象关于x轴对称,得到新的函数图象C,若直线y=x+k与图象C始终有3个交点,求满足条件的k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形(阴影部分)和一个长方形(阴影部分)得到一个“囧”字图案,设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
(1)用含a、x、y的式子表示“囧”的面积;
(2)当a=12,x=7,y=4时,求该图形面积的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com