
 如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF
如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF分析 (1)连接DB,CF,利用对角线互相平分的四边形是平行四边形可得四边形CDBF是平行四边形,进而可得CD=BF;
(2)由(1)可得CD∥FB,再利用三角形中位线定理可得DF∥AB,根据两组对边分别平行的四边形是平行四边形可得结论.
解答 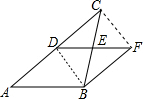 证明:(1)连接DB,CF,
证明:(1)连接DB,CF,
∵DE是△ABC的中位线,
∴CE=BE,
∵EF=ED,
∴四边形CDBF是平行四边形,
∴CD=BF;
(2)∵四边形CDBF是平行四边形,
∴CD∥FB,
∴AD∥BF,
∵DE是△ABC的中位线,
∴DE∥AB,
∴DF∥AB,
∴四边形ABFD是平行四边形.
点评 此题主要考查了平行四边形的判定和性质,以及三角形中位线定理,关键是掌握对角线互相平分的四边形是平行四边形,两组对边分别平行的四边形是平行四边形.


科目:初中数学 来源: 题型:选择题
| A. | AO=CO | B. | AO=BO | C. | AO⊥BO | D. | AB⊥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )| A. | 常数k<-1 | |
| B. | 在每个象限内,y随x的增大而增大 | |
| C. | 若P(x,y)在图象上,则P′(-x,-y)也在图象上 | |
| D. | 若A(-1,m),B(2,n)在图象上,则m>n |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届广东省佛山市顺德区九年级第一次模拟考试数学试卷(解析版) 题型:单选题
如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
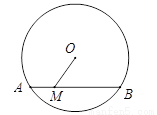
A. 3≤OM≤5 B. 4≤OM≤5 C. 3<OM<5 D. 4<OM<5
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com