
��ͼ���ı���ABCD�����Σ��Խ���AC��BD���ڵ�O����AC=80��BD=60������M��N�ֱ���ÿ��1����λ���ٶȴӵ�A��Dͬʱ�������ֱ���A��O��D��D��A�˶�������N�����Aʱ��M��Nͬʱֹͣ�˶������˶�ʱ��Ϊt�룮
��1��������ABCD���ܳ���
��2���ǡ�DMN�����ΪS����S����t�Ľ���ʽ������S�����ֵ��
��3����t=30��ʱ�����߶�OD�Ĵ�ֱƽ�������Ƿ���ڵ�P��ʹ�á�DPO=��DON�������ڣ������ĵ�P�м������������P���߶�OD�ľ��룻�������ڣ���˵�����ɣ�
�⣺��1��������ABCD�У�
��AC��BD��AC=80��BD=60���� ��
��
������ABCD���ܳ�Ϊ200��
��2������M��MP��AD��������P��
�ٵ�0��t��40ʱ�����ͼ1��
�� ��
��
��MP=AM•sin��OAD= t��
t��
S= DN•MP=
DN•MP= ��t��
��t�� t=
t= t2��
t2��
�ڵ�40��t��50ʱ�����ͼ2��MD=70��t��
�� ��
��
��MP= ��70��t����
��70��t����
��S��DMN= DN•MP=
DN•MP= ��t��
��t�� ��70��t��=
��70��t��= t2+28t=
t2+28t= ��t��35��2+490��
��t��35��2+490��
��S����t�Ľ���ʽΪ ��
��
��0��t��40ʱ��S��t�����������t=40ʱ�����ֵΪ480��
��40��t��50ʱ��S��t���������С�����ֵ������480��
����������S�����ֵΪ480��
��3������2����P��ʹ�á�DPO=��DON��
���ͼ3��ʾ������N��NF��OD�ڵ�F��
��NF=ND•sin��ODA=30�� =24��
=24��
DF=ND•cos��ODA=30�� =18��
=18��
��OF=12���� ��
��
����NOD��ƽ���߽�NF�ڵ�G������G��GH��ON�ڵ�H��
��FG=GH��
��S��ONF= OF•NF=S��OGF+S��OGN=
OF•NF=S��OGF+S��OGN= OF•FG+
OF•FG+ ON•GH=
ON•GH= ��OF+ON��•FG��
��OF+ON��•FG��
�� ��
��
�� ��
��
��OD�д�����OD�Ľ���ΪK���ɶԳ��Կ�֪����DPK= ��DPO=
��DPO= ��DON=��FOG��
��DON=��FOG��
�� ��
��
��PK= ��
��
�������εĶԳ��Կ�֪�����߶�OD���·��������P����OD��ԳƵĵ�P�䡣
�����������P��OD�ľ��붼��
���������������1�����ݹ��ɶ��������ε����ʣ�������ε��ܳ���
��2���ڶ���M��N�˶������У��ٵ�0��t��40ʱ�����ͼ1��ʾ���ڵ�40��t��50ʱ�����ͼ2��ʾ���ֱ����S�Ĺ�ϵʽ��Ȼ�����ö��κ���������������ֵ��
��3�����ͼ3��ʾ����Rt��PKD�У�DK�����������ֻ�����tan��DPK���ɣ�Ϊ�ˣ��ڡ�ODM�У��������ߣ�����Rt��OND������NODƽ����OG�����GOF=��DPK����Rt��OGF�У����tan��GOF��ֵ���Ӷ���������
���⣺��ͼ4��ʾ����ON�Ĵ�ֱƽ���ߣ���OD�Ĵ�ֱƽ����EF�ڵ�I�����ӽ�OI��IN������N��NG��OD��NH��EF������ֱ�ΪG��H��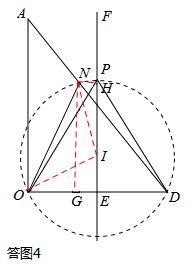
��t=30ʱ��DN=OD=30����֪��DNG�ס�DAO��
�� ����
���� ��
��
��NG=24��DG=18��
��EF��ֱƽ��OD����OE=ED=15��EG=NH=3��
��OI=R��EI=x����
��Rt��OEI����R2=152+x2 ��
��Rt��NIH����R2=32+��24��x��2 ��
�ɢ١��ڿɵã� ��
��
��PE=PI+IE= ��
��
���ݶԳ��Կɵã���BD�·�������һ����P��Ҳ����������
�����������P����OD�ľ��붼�� ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
Ϊ����ʵ����Ժ��ָʾ����ij�ط�������̨��һϵ�С���ũ���Ż����ߣ�ʹũ�������������ӣ�ijũ����������һ��ũ��Ʒ����֪���ֲ�Ʒ�ijɱ���Ϊÿǧ��20Ԫ���г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ������¹�ϵ��y=��2x+80�������ֲ�Ʒÿ�����������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ��
��2���ò�Ʒ���ۼ۶�Ϊÿǧ�˶���Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��3�������۲��Ź涨���ֲ�Ʒ�����ۼ۲�����ÿǧ��28Ԫ����ũ����Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊÿǧ�˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=��1��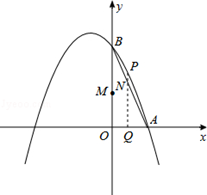
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2������Q�ӵ�O��������ÿ��1����λ���ȵ��ٶ����߶�OA���˶���ͬʱ����M��M��O�������ÿ��3����λ���ȵ��ٶ����߶�OB���˶�������Q��x��Ĵ��߽��߶�AB�ڵ�N�����������ڵ�P�����˶���ʱ��Ϊt�룮
�ٵ�tΪ��ֵʱ���ı���OMPQΪ���Σ�
�ڡ�AON�ܷ�Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2013���Ĵ�����12�֣���ͼ�����κ���y=ax2+bx+c��ͼ��Ķ���C������Ϊ��0����2������x����A��B���㣬����A����1��0����ֱ��l��x=m��m��1����x�ύ��D��
��1������κ����Ľ���ʽ��B�����ꣻ
��2����ֱ��l���ҵ�P��P�ڵ�һ���ޣ���ʹ����P��D��BΪ���������������B��C��OΪ��������������ƣ����P�����꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£������������Ƿ���ڵ�һ�����ڵĵ�Q��ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Σ�������ڣ��������Q�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪��������x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C��0��3����
��1���������ߵĽ���ʽ��
��2���������ߵĶ���ΪD������Գ�����Ҳ�����������Ƿ���ڵ�P��ʹ�á�PDC�ǵ��������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3����M����������һ�㣬��B��C��D��MΪ������ı�����ֱ�����Σ��������M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2013���Ĵ��㰲10�֣���ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c����A��B��C���㣬��֪��A����3��0����B��0��3����C��1��0����
��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣬�������A��B�غϣ�������P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D��
�ٶ���P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
������PA����APΪ����ͼʾһ���������APMN�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������M��Nǡ�����������߶Գ�����ʱ�������Ӧ��P������꣮������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��y���ڵ�C��0��4�����Գ���x=2��x�ύ�ڵ�D������ΪM����DM=OC+OD��
��1����������ߵĽ���ʽ��
��2�����P��x��y���ǵ�һ�����ڸ��������ϵ�һ�����㣬��PCD�����ΪS����S����x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3���ڣ�2���������£���������P��ֱ��PE��y�ύ�ڵ�E���Ƿ������O��P��EΪ��������������OPDȫ�ȣ������ڣ������ֱ��PE�Ľ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y=��x2+4��x�ύ��A��B���㣬��y�ύ��C�㣬��P���������ϵ�һ���������ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD����ֱ��BC�ڵ�E��
��1�����A��B��C�������ֱ��BC�Ľ���ʽ��
��2�����ODE��������ֵ����Ӧ�ĵ�E�����ꣻ
��3���Ƿ�����Ե�P��O��DΪ��������������OAC���ƣ������ڣ��������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У��ı���ABCO�����Σ�����A��6��0����B��3�� ����C��1��
����C��1�� ��������P�ӵ�O��ÿ��2����λ���ٶ����A�˶�������QҲͬʱ�ӵ�B��B�� C��O����·��ÿ��1����λ���ٶ����O�˶�������P����A��ʱ����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ��Ϊt���룩.
��������P�ӵ�O��ÿ��2����λ���ٶ����A�˶�������QҲͬʱ�ӵ�B��B�� C��O����·��ÿ��1����λ���ٶ����O�˶�������P����A��ʱ����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ��Ϊt���룩.
��1����A��B��C����������ߵĽ���ʽ��
��2������Q��CO�����˶�ʱ�����OPQ�����S��ʱ��t�ĺ�����ϵʽ��
��3����O��P��QΪ������������ܹ���ֱ�������������ܣ������t��ֵ�������ܣ���˵�����ɣ�
��4������A��B��C����������ߵĶԳ��ᡢֱ��OB��PQ�ܹ�����һ�������ܣ��������ʱt��ֵ����Χ���������ܣ���˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com