(1)证明:(方法一)∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∵E、F分别的边AD、BC的中点.
∴ED=BF,
∴四边形DEBF是平行四边形,
∴BE=DF;
(方法二)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC且∠A=∠C,
∵E、F分别的边AD、BC的中点,
∴AE=CF,
在△AEB和△CFD中
∵
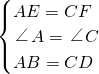
,
∴△ABE≌△CDF(SAS),
∴BE=DF;
(2)解:由(1)中的方法一可知四边形DEBF是平行四边形,故BE∥DF.
分析:(1)方法一:首先根据四边形ABCD是平行四边形,可得AD∥BC,且AD=BC,再证明四边形DEBF是平行四边形,即可根据平行四边形的性质得到BE=DF;
方法二:首先根据四边形ABCD是平行四边形,可得AB=CD,AD=BC且∠A=∠C,再根据E、F分别的边AD、BC的中点,可得AE=CF,再利用SAS证明△ABE≌△CDF,根据全等三角形的性质可得结论;
(2)根据(1)中证明方法一可直接得到BE∥DF.
点评:此题主要考查了全等三角形的判定,平行四边形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.平行四边形的判定是结合平行四边形的性质证明线段和角相等的重要工具,同学们要熟练掌握平行四边形的判定方法.

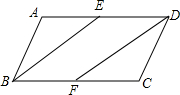
 如图,E、F分别是平行四边形ABCD的边AD、BC的中点.
如图,E、F分别是平行四边形ABCD的边AD、BC的中点.
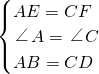 ,
,

 阅读快车系列答案
阅读快车系列答案 (2011•延平区质检)如图,A、B分别是函数y=
(2011•延平区质检)如图,A、B分别是函数y=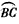 的中点,DE⊥AC平点E,DE=6cm,CE=2cm。
的中点,DE⊥AC平点E,DE=6cm,CE=2cm。