
����Ŀ��Ϊ��Ӧ���漤�ҵ��г�����Ҫ��ij������2016��1���ҿ�ʼ�������������߽���Ϊ��5���µ��������죬�����ڼ����������ʱ��ɷ���������5�µ�ʼ�ָ�ȫ����������ÿ�µ�����ǰһ��������10��Ԫ����2016��1��Ϊ��1���£���x���µ�����Ϊy��Ԫ����ͼ����ͼ��ʾ���Խ���������⣺ 
��1���ֱ���ù����������߽�����������ǰ��y��x֮��ĺ�����ϵʽ��
��2�����ڼ�����ʱ���ù�������������ٴδﵽ100��Ԫ��
��3��������������50��Ԫʱ��Ϊ�ù������ʽ�����ڣ��ʸù����ʽ�����ڹ��м����£�
���𰸡�
��1���⣺������ã���ǰ5������y��x�Ļ��ǹ�ϵʽΪy= ![]() ����x=1��y=3����ã�k=100��
����x=1��y=3����ã�k=100��
��y��x֮��ĺ�����ϵʽΪy= ![]() ��
��
��x=5�����y= ![]() =20��
=20��
��������5�·��Ժ�y��x�ĺ�����ϵʽΪy=10x+b��
��x=5��y=20����ã�20=10��5+b��
��b=��30��
��y��x֮��ĺ�����ϵʽΪy=10x��30
��2���⣺������ã���y=100����y=10x��30��100=10x��30����ã�x=13��
�ൽ��13����ʱ���ù�������������ٴδﵽ100��Ԫ
��3���⣺����y= ![]() ��y=50ʱ��x=2��
��y=50ʱ��x=2��
��k=100��0��y��x���������С����x��2ʱ��y��50������y=10x��30����y=50ʱ��x=8��
��k=10��0��y��x�����������x��8ʱ��y��50����2��x��8ʱ������������50��Ԫ����ù����ʽ�����ڹ���5����
����������1�����������з��̼��ɵõ���������ʽ����2����y=100����y=10x��30���ɵõ����ۣ���3������y= ![]() ��y=50ʱ���õ�x=2���õ�x��2ʱ��y��50������y=10x��30����y=50ʱ���õ�x=8�����ǵõ����ۣ�
��y=50ʱ���õ�x=2���õ�x��2ʱ��y��50������y=10x��30����y=50ʱ���õ�x=8�����ǵõ����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� ![]() ABC�У�ADƽ��
ABC�У�ADƽ�� ![]() BAC�������²�����ͼ��
BAC�������²�����ͼ��
��һ�����ֱ��Ե�A��DΪԲ�ģ��Դ��� ![]() AD�ij�Ϊ�뾶��AD������������������M��N��
AD�ij�Ϊ�뾶��AD������������������M��N��
�ڶ���������MN�ֱ�AB��AC�ڵ�E��F��
������������DE��DF.
��BD=6��AF=4��CD=3����BE�ij��ǣ� ��.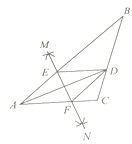
A.2
B.4
C.6
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
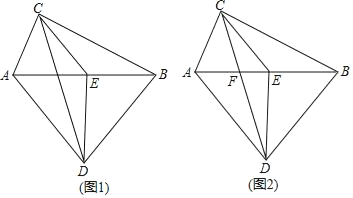
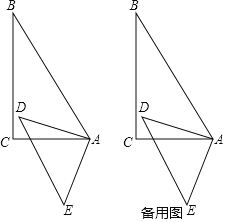
����Ŀ����ͼ����֪AC��BC��AD��BD��EΪAB���е㣬
��1����ͼ1����֤����ECD�ǵ��������Σ�
��2����ͼ2��CD��AB����ΪF����AD=BD��EF=3��DE=4����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABC�У���C=90�㣬AC=BC��ADƽ�֡�CAB��BC��D��DE��BA��E��AB=6���ף�����DEB���ܳ���_____���ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��CD���е㣬AE���ӳ��߽�BC���ӳ�����F���ֱ�����AC��DF������������⣺ 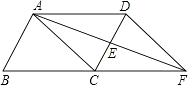
��1����֤����ADE�ա�FCE��
��2����DCƽ�֡�ADF����ȷ���ı���ACFD��ʲô�����ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��˫����
��˫����![]() ����
����![]() ���㣬�ҵ�
���㣬�ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��

��1����![]() ��ֵ��
��ֵ��
��2����˫����![]() ��һ��
��һ��![]() ��������Ϊ8����
��������Ϊ8����![]() �������
�������
��3����ԭ��![]() ����һ��ֱ��
����һ��ֱ��![]() ��˫����
��˫����![]() ��
��![]() ���㣨
���㣨![]() ���ڵ�һ���ޣ������ɵ�
���ڵ�һ���ޣ������ɵ�![]() Ϊ������ɵ��ı������Ϊ
Ϊ������ɵ��ı������Ϊ![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺ֱ��l1��l2�ཻ�ڵ�O������ƽ��������һ��M����M��ֱ��l1��l2�ľ���ֱ�Ϊp��q���������ʵ���ԣ�p��q���ǵ�M�ġ��������ꡱ�������������壬���������ꡱ�ǣ�1��2���ĵ�ĸ����ǣ�������
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y= ![]() x2+2x��x���ཻ��O��B������ΪA������OA��
x2+2x��x���ཻ��O��B������ΪA������OA��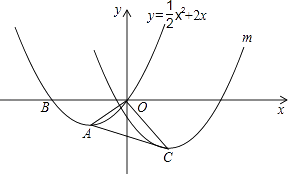
��1�����A������͡�AOB�Ķ�����
��2������������y= ![]() x2+2x����ƽ��4����λ��������ƽ��2����λ���õ�������m���䶥��Ϊ��C������OC��AC���ѡ�AOC��OA���۵õ��ı���ACOC�䣮���ж�����״����˵�����ɣ�
x2+2x����ƽ��4����λ��������ƽ��2����λ���õ�������m���䶥��Ϊ��C������OC��AC���ѡ�AOC��OA���۵õ��ı���ACOC�䣮���ж�����״����˵�����ɣ�
��3���ڣ�2��������£��жϵ�C���Ƿ���������y= ![]() x2+2x�ϣ���˵�����ɣ�
x2+2x�ϣ���˵�����ɣ�
��4������PΪx���ϵ�һ�����㣬��̽����������m���Ƿ���ڵ�Q��ʹ�Ե�O��P��C��QΪ������ı�����ƽ���ı��Σ���OCΪ���ı��ε�һ���ߣ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ� ���ο���ʽ�����κ���y=ax2+bx+c��a��0��ͼ��Ķ�������Ϊ�� ![]() ��
�� ![]() �����Գ�����ֱ��x=
�����Գ�����ֱ��x= ![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֱ�����dzߵ�60��Ǻ�90��ǵĶ���A������һ�𣮽����dz�ADE�Ƶ�A��ת����ת���������dz�ADE�ı�ADʼ���ڡ�BAC���ڲ�����ת�����У�̽����
��1����BAE���CAD�Ķ����к�������ϵ����˵�����ɣ�
��2����˵����CAE����BAD��30�㣻
��3������BAD�͡�CAE��ƽ����AM��AN������ת�����С�MAN��ֵ�Ƿ����仯�������䣬����������ֵ�����仯��������仯��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com