
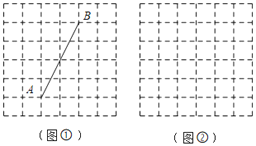
【题目】如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点.
(1)在图①中,线段AB的长度为 ;若在图中画出以C为直角顶点的Rt△ABC,使点C在格点上,请在图中画出所有点C;
(2)在图②中,以格点为顶点,请先用无刻度的直尺画正方形ABCD,使它的面积为13;再画一条直线PQ(不与正方形对角线重合),使PQ恰好将正方形ABCD的面积二等分(保留作图痕迹).
科目:初中数学 来源: 题型:
【题目】三位老师周末到某家电专卖店购买冰箱和空调,正值该专卖店举行“迎新春、大优惠”活动,具体优惠情况如下表:
购物总金额(原价) | 折扣率 |
不超过3000元的部分 | 九折 |
超过3000元但不超过5000元的部分 | 八折 |
超过5000元的部分 | 七折 |
(1)李老师所购物品的原价是6000元,李老师实际付 元
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的"距离",记作d(M,N) . 特别的,当图形M,N有公共点时,记作d(M,N)=0.一次函数y=kx+2的图像为L,L 与y 轴交点为D, △ABC中,A(0,1),B(-1,0),C(1,0).
(1)求d(点 D , △ABC)= ;当k=1时,求d( L , △ABC)= ;
(2)若d(L, △ABC)=0.直接写出k的取值范围;
(3)函数y=x+b的图像记为W , 若d(W,△ABC) ![]() 1 ,求出b的取值范围.
1 ,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
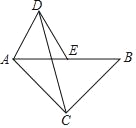
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AB=4,点E为AB的中点.以AE为边作等边△ADE(点D与点C分别在AB的异侧),连接CD.则△ACD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,

(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,观察函数y=|x|的图象,写出它的两条的性质;
(2)在图1中,画出函数y=|x-3|的图象;
根据图象判断:函数y=|x-3|的图象可以由y=|x|的图象向 平移 个单位得到;
(3)①函数y=|2x+3|的图象可以由y=|2x|的图象向 平移 单位得到;
②根据从特殊到一般的研究方法,函数y=|kx+3|(k为常数,k≠0)的图象可以由函数y=|kx|(k为常数,k≠0)的图象经过怎样的平移得到.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣8)﹣(﹣15)+(﹣9)﹣(﹣12)
(2)7![]() +(﹣6.5)+3
+(﹣6.5)+3![]() +(﹣1.25)+2
+(﹣1.25)+2![]()
(3)(﹣81)÷(﹣2![]() )×
)×![]() ÷(﹣8)
÷(﹣8)
(4)![]()
(5)![]()
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
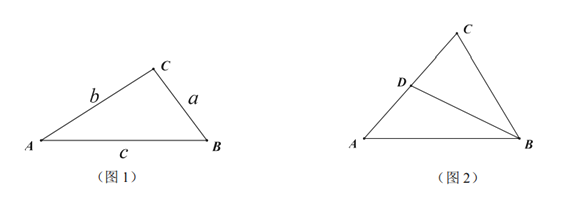
【题目】如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.
(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com