
【题目】已知:CP是等边△ABC的外角∠ACE的平分线,点D在边BC上,以D为顶点,DA为一条边作∠ADF=60°,另一边交射线CP于F
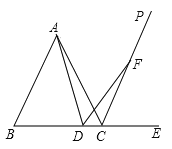
(1)求证:AD=FD
(2)若AB=2,BD=x,DF=y,求y关于x的函数解析式
(3)若点D在线段BC的延长线上,(1)中的结论还一定成立吗?若成立,请证明.
【答案】(1)见解析;(2)![]() ;(3)成立,证明见解析.
;(3)成立,证明见解析.
【解析】
(1)利用外角平分线得:∠ACP=∠PCE=60°,证明A、D、C、F四点共圆,从而得出△ADF是等边三角形,所以AD=FD;
(2)作AM⊥BC于M.证明AD2=AEAB,即可解决问题;
(3)同(1)得:A、C、D、F四点共圆,则△ADF 是等边三角形,所以AD=FD.
(1)连接AF,
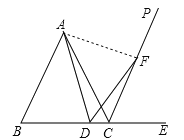
∵∠ACB=60°,
∴∠ACE=120°,
∵CP平分∠ACE,
∴∠ACP=∠PCE=60°,
∴∠ADF=∠ACP=60°,
∴A、D、C、F四点共圆,
∴∠AFD=∠ACB=60°,
∴∠ADF=∠AFD=60°,
∴∠DAF=60°,
∴△ADF是等边三角形,
∴AD=FD;
(2)过A作AM⊥BC于M,如图,
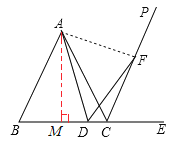
∵△ABC是等边三角形,
∴BC=AB=2,BM=![]() BC=1,
BC=1,
∴AM=![]()
∵BD=x,
∴MD=x-1,
∵△ADF是等边三角形,
∴AD=DF=y,
在Rt△AMD中,![]()
∴![]() ,即
,即![]() ;
;
(3)如图,
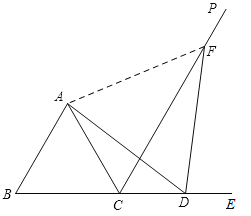
同(1)得:∠ADF=∠ACF=60°,
∴A、C、D、F四点共圆,
∴∠FAD=∠FCD=60°,
∴∠AFD=60°,
∴△ADF 是等边三角形,
∴AD=FD.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=2x2﹣8x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,则m的值为( )
A. 8 B. ﹣10 C. ﹣42 D. ﹣24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“感冒”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后y与x成反比例如图。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:
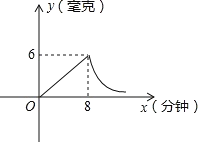
(1)药物燃烧时,y关于x的函数关系式为___,自变量x的取值范围是___;药物燃烧后y关于x的函数关系式为___.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过___分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病毒,那么此次消毒有效吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
① 当x取什么值时,y>0 ?
② 当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②DE长度的最小值为4;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论是( )
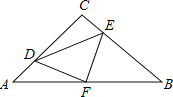
A.①②③B.①③C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
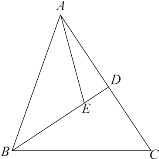
【题目】如图,△ABC中,AE=BE,∠AED =∠ABC.
(1)求证:BD平分∠ABC;
(2)若AB = CB,∠AED =4∠EAD,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.

![]() 求这条直线的函数关系式及点
求这条直线的函数关系式及点![]() 的坐标.
的坐标.
![]() 在
在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
![]() 过线段
过线段![]() 上一点
上一点![]() ,作
,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限,点
在第一象限,点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com