
分析 (1)根据图上信息可以得出甲乙商品之间价格之间的等量关系,即可得出方程组求出即可;
(2)把商店的销售利润表示成n的函数,根据函数的性质即可求解.
解答 解:(1)假设甲、乙两种商品的进货单价各为x,y元,则甲的零售价是(x+2)元,乙的零售价是(2y-3)元.
根据题意得:
$\left\{\begin{array}{l}{x+y=10}\\{2(x+2)+3(2y-3)=31}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$,
∴甲、乙零售单价分别为6元和4元;
(2)甲、乙两种商品的零售单价都涨n元,则甲、乙商品的销售量分别是(500-100n)、(200-100n)件,甲的每件利润是(2+n)元,乙每件的利润是2y-3-y+n=y-3+n=1+n元.
则商店的每天的销售利润w=(500-100n)(2+n)+(200-100n)(1+n),即w=-200n2+400n+1200,
则当n=-$\frac{400}{2×(-200)}$=1时,w最大,最大值是:1400元.
点评 此题主要考查了一元二次方程的应用,此题比较典型也是近几年中考中热点题型,注意表示总利润时表示出商品的单件利润和所卖商品件数是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
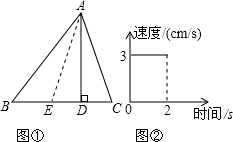 如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②
如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型智能手表 | B型智能手表 | |
| 进价 | 1300元/只 | 1500元/只 |
| 售价 | 今年的售价 | 2300元/只 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
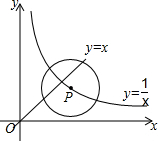 如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )
如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )| A. | 1≤x≤$\sqrt{2}$ | B. | $\sqrt{2}-1≤x≤\sqrt{2}$ | C. | $\sqrt{2}-1≤x≤1$ | D. | $\sqrt{2}-1≤x≤\sqrt{2}+1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com