
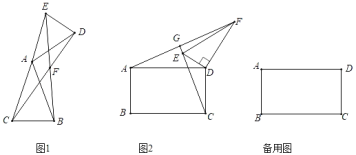
【题目】(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=30°,连接CD,BE交于点F.![]() = ;∠BFD= ;
= ;∠BFD= ;
(2)如图2,在矩形ABCD和△DEF中,AB=![]() AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求
AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求![]() 的值及∠AGC的度数,并说明理由.
的值及∠AGC的度数,并说明理由.
(3)在(2)的条件下,将△DEF绕点D在平面内旋转,AF,CE所在直线交于点P,若DE=1,AD=![]() ,求出当点P与点E重合时AF的长.
,求出当点P与点E重合时AF的长.
【答案】(1)1,150°;(2)![]() ,∠AGC=90°,见解析;(3)6
,∠AGC=90°,见解析;(3)6
【解析】
(1)利用SAS判断出![]() 得出CD=BE,再用数据线的外角和三角形的内角和定理,即可得出结论.
得出CD=BE,再用数据线的外角和三角形的内角和定理,即可得出结论.
(2)先判断出![]() 进而判断出△ADF∽△CDE,即可得出结论.
进而判断出△ADF∽△CDE,即可得出结论.
(3)先求出EF=2,设出CE,进而表示出AE,分两种情况:用勾股定理求出CE,即可得出结论.
解:(1)∵∠BAC=∠DAE=30°,
∴∠BAC+∠BAD=∠DAE+∠BAD,
∴∠CAD=∠BAE,
∵AC=AB,AD=AE,
∴△CAD≌△BAE(SAS),
∴CD=BE,
∴![]() =1,
=1,
∵△CAD≌△BAE(SAS),
∴∠ACD=∠ABE,
∴∠BFD=∠DCB+∠CBE=∠DCB+∠ABE+∠ABC=∠DCB+∠ACD+∠ABC=∠ACB+∠ABC=180°﹣∠BAC=150°,
故答案为1,150°;
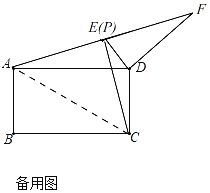
(2)如图2,∵四边形ABCD是矩形,
∴∠ADC=90°,AB=CD,
∵AB=![]() AD,
AD,
∴![]() =
=![]() ,
,
在Rt△DEF中,∠DEF=60°,
∴tan∠DEF=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵∠EDF=90°=∠ADC,
∴∠ADF=∠CDE,
∴△ADF∽△CDE,
∴![]() ,∠DAF=∠DCE,
,∠DAF=∠DCE,
AD与CD的交点记作点O,
∵∠DCE+∠COD=90°,
∴∠DAF+∠AOG=90°,
∴∠AGC=90°;
(3)如备用图,
连接AC,在Rt△ADC中,AD=![]() ,
,
∴AB=![]() AD=
AD=![]() ,
,
根据勾股定理得,AC=2![]() ,
,
由(2)知,![]() ,
,
∴AF=![]() CE,
CE,
设CE=x.则AF=![]() x,
x,
在Rt△DEF中,∠DEF=60°,DE=1,
∴EF=2,
∴AE=AF﹣EF=![]() x﹣2,
x﹣2,
由(2)知,∠AEC=90°,
在Rt△ACE中,AE2+CE2=AC2,
∴(![]() x﹣2)2+x2=28,
x﹣2)2+x2=28,
∴x=﹣![]() (舍)或x=2
(舍)或x=2![]() ,
,
∴AF=![]() x=6.
x=6.


科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源,生活垃圾一般按如图所示A、B、C、D四种分类方法回收处理,某城市环保部门为了提高宣传实效,抽样调查、统计了部分居民小区一段时间内生活垃圾的分类处理情况,并将调查统计结果绘制成如下两幅不完整的统计图表:
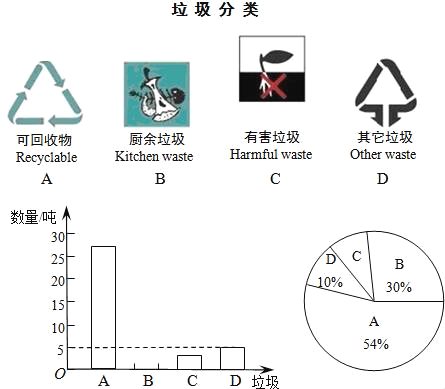
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q.则在点P运动过程中,切线CQ的长的最大值为_____.
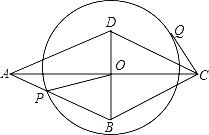
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
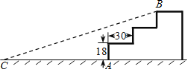
A.270cmB.210cmC.180cmD.96cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张正面分别写有数字:﹣3,﹣2,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不小于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为m的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为n的值,请用列表法或画树状图法,求点Q(m,n)在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,矩形
,矩形![]() 在直线
在直线![]() 上绕其右下角的顶点
上绕其右下角的顶点![]() 向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转100次后顶点
向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转100次后顶点![]() 在整个旋转过程中所经过的路程之和是_________.
在整个旋转过程中所经过的路程之和是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为( )
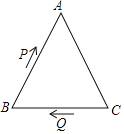
A.![]() sB.
sB.![]() sC.
sC.![]() s或
s或![]() sD.以上均不对
sD.以上均不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为____.
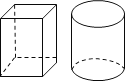
查看答案和解析>>
科目:初中数学 来源: 题型:
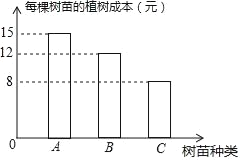
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com