练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．等式$\sqrt{\frac{a-2}{a+1}}$=$\frac{\sqrt{a-2}}{\sqrt{a+1}}$成立的条件是（　　）
    A．a≠1B．a＞1C．a≥2D．-1＜a≤2

    分析 直接利用二次根式的性质得出各式的符号，进而求出答案．

    解答 解：∵等式$\sqrt{\frac{a-2}{a+1}}$=$\frac{\sqrt{a-2}}{\sqrt{a+1}}$成立，
    ∴$\left\{\begin{array}{l}{a-2≥0}\\{a+1＞0}\end{array}\right.$，
    解得：a≥2．
    故选：C．

    点评 此题主要考查了二次根式的性质，正确掌握二次根式的定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．点M（2，-3）到x轴的距离是（　　）
    A．2B．-3C．3D．以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，在长方形ABCD中，放入六个形状大小相同的长方形，所标尺寸如图所示，请你利用方程组的思想方法求出图中阴影部分面积是多少cm2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

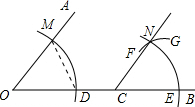    9．已知，点C在∠AOB的OB边上，用尺规过点C作CN∥OA，作图痕迹如图所示，下列对弧FG的描述，正确的是（　　）
    A．以点C为圆心，OD的长为半径的弧B．以点C为圆心，OM的长为半径的弧
    C．以点E为圆心，DM的长为半径的弧D．以点E为圆心，CE的长为半径的弧

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

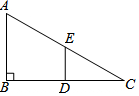    16．如图，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，当△EDC旋转到A，D，E三点共线时，线段BD的长为4$\sqrt{5}$或$\frac{12}{5}\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．一个水分子的质量约是3×10-26kg，那么8个水分子的质量用科学记数法表示为（　　）
    A．24×10-26kgB．2.4×10-25kgC．0.24×10-24kgD．2.4×10-24kg

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，已知直线y=mx+n与反比例函数y=$\frac{k}{x}$交于A、B两点，点A在点B的左边，与x轴、y轴分别交点C、点D，AE⊥x轴于E，BF⊥y轴于F．
    （1）若m=k，n=0，求A、B；两点的坐标；
    （2）如图1，若A（x1，y1）、B（x2，y2），写出y1+y2与n的大小关系，并证明；
    （3）如图2，M、N分别为反比例函数y=$\frac{b}{x}$图象上的点，AM∥MN∥x轴．若$\frac{1}{AM}$+$\frac{1}{BN}$=$\frac{5}{3}$，且AM、BN之间的距离为5，则k-b=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

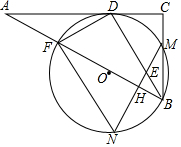    10．如图，在Rt△ABC中，∠C=90°，BD为∠ABC的平分线，DF⊥BD交AB于点F，△BDF的外接圆⊙O与边BC相交于点M，过点M作AB的垂线交BD于点E，交⊙O于点N，交AB于点H，连接FN．
    （1）求证：AC是⊙O的切线；
    （2）若AF=1，tan∠N=$\frac{4}{3}$，求⊙O的半径r的长；
    （3）在（2）的条件下，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．圆的半径为r厘米，若半径增加3厘米，则新圆的面积比原来圆的面积增加了（　　）
    A．9π平方厘米B．3π（2r-3）平方厘米C．3π（2r+3）平方厘米D．π（r+3）2平面厘米

    查看答案和解析>>

    同步练习册答案