
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
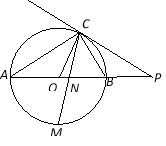
(1)求证:PC是⊙O的切线;
(2)求证:BC=AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、8.
【解析】
试题分析:(1)、根据OA=OC得出∠A=∠ACO,根据∠COB=2∠A,,∠COB=2∠PCB,则∠A=∠ACO=∠PCB,根据AB为直径得出∠ACO+∠OCB=90°,则∠∠PCB+∠OCB=90°,得出切线;(2)、根据AC=PC得出∠A=∠P,则∠A=∠ACO=∠PCB=∠P,根据∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB得出∠COB=∠CBO,然后得出答案;(3)、连接AM、BM,根据M是弧的中点得出∠ACM=∠BCM,根据∠ACM=∠ABM得到∠BCM=∠ABM,从而得出△MBN∽△MCB,根据相似比得出BM2=MN·MC;根据等腰直角△ABM中AB的长度得出AM和BM的长度,然后计算.
试题解析:(1)、如图∵OA=OC,∴∠A=∠ACO,
又∵∠COB=2∠A,∠COB=2∠PCB,∴∠A=∠ACO=∠PCB,又∵AB是⊙O的直径, ∴∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,∴∠PCO=90°,即OC⊥CP, 而OC是⊙O的半径,∴PC是⊙O的切线;.
(2)、∵AC=PC,∴∠A=∠P, ∴∠A=∠ACO=∠PCB=∠P, 又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,∴BC=OC,∴BC=AB;
(3)、连接MA,MB,∵点M是弧AB的中点, ∴![]() ,∴∠ACM=∠BCM,∵∠ACM=∠ABM,∴∠BCM=∠ABM,
,∴∠ACM=∠BCM,∵∠ACM=∠ABM,∴∠BCM=∠ABM,
又∵∠BMN=∠BMC,∴△MBN∽△MCB,∴=, ∴BM2=MN·MC,
又∵AB是⊙O的直径,![]() ,∴∠AMB=90°,AM=BM,
,∴∠AMB=90°,AM=BM,
∴AB=4,∴BM=2,∴MN·MC=BM2=(2)2=8


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=﹣x+4于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.

(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
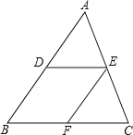
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用反证法证明命题“四边形中至少有一个角是钝角或直角”时,应假设( )
A. 四边形中至多有一个内角是钝角或直角
B. 四边形中所有内角都是锐角
C. 四边形的每一个内角都是钝角或直角
D. 四边形中所有内角都是直角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①平面内过一点有且只有一条直线和已知直线垂直;②垂线段最短;③平行于同一条直线的两条直线也互相平行;④同位角相等.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=(k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.

(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏。游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的。规定:①玩家只能将小兔从A、B两个出入口放入;
②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元。
(1)、问小美得到小兔玩具的机会有多大?
(2)、假设有100人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com