
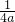 )和到定直线
)和到定直线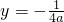 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,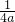 )叫做抛物线y=ax2的焦点,定直线
)叫做抛物线y=ax2的焦点,定直线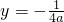 叫做抛物线y=ax2的准线.
叫做抛物线y=ax2的准线.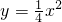 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;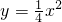 图象上,O为坐标原点,求等边三角形的边长;
图象上,O为坐标原点,求等边三角形的边长;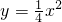 上的一个动点,F为抛物线
上的一个动点,F为抛物线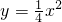 的焦点,P(1,3)为定点,求MP+MF的最小值.
的焦点,P(1,3)为定点,求MP+MF的最小值.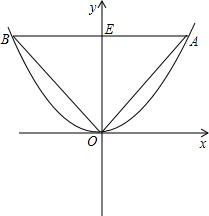
 ∠AOB=30°,
∠AOB=30°, x,
x, x)代入函数解析式,可得
x)代入函数解析式,可得 x=
x= x2,
x2, ,
, ,12),三角形的边长=OA=
,12),三角形的边长=OA=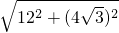 =8
=8 .
.
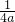 ),准线方程为
),准线方程为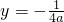 ,即可得出答案.
,即可得出答案. |x|,代入可得出x和y的值,也可求出等边三角形的边长.
|x|,代入可得出x和y的值,也可求出等边三角形的边长.

 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源:2008年北京市石景山区初三二模数学试题 题型:044
研究发现,二次函数y=ax2(a≠0)图象上任何一点到定点(0,![]() )和到定直线
)和到定直线![]() 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,![]() )叫做抛物线y=ax2的焦点,定直线
)叫做抛物线y=ax2的焦点,定直线![]() 叫做抛物线u=ax2的准线.
叫做抛物线u=ax2的准线.
(1)写出函数![]() 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数![]() 图象上,O为坐标原点,
图象上,O为坐标原点,
求等边三角形的边长;
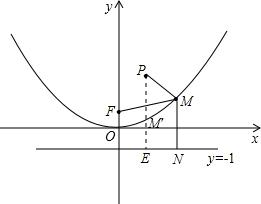
(3)M为抛物线![]() 上的一个动点,F为抛物线
上的一个动点,F为抛物线![]() 的焦点,P(1,3)
的焦点,P(1,3)
为定点,求MP+MF的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com