
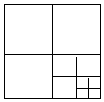
 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2017}$ | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{1}{4}$)2017 | D. | 1-($\frac{1}{4}$)2017 |
分析 先计算出正方形的面积为1,根据题意易得第1次操作后右下角的小正方形面积=$\frac{1}{4}$,第2次操作后右下角的小正方形面积=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,第3次操作后右下角的小正方形面积=($\frac{1}{4}$)3,于是可得到n次操作后右下角的小正方形面积为$\frac{1}{4}$的n次方,然后把n=2014代入即可得到答案.
解答 解:正方形的面积=1×1=1,
∵第1次操作后右下角的小正方形面积=$\frac{1}{4}$,
第2次操作后右下角的小正方形面积=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,
第3次操作后右下角的小正方形面积=($\frac{1}{4}$)3,
…
∴第2017次操作后右下角的小正方形面积=($\frac{1}{4}$)2017.
故选C.
点评 本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | (-3a)2+4a2=a2 | B. | 3a2-(-2a)2=-a2 | C. | 3a•4a2=12a2 | D. | (3a2)2÷4a2=$\frac{3}{4}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=3,x2=-3 | B. | x1=x2=0 | C. | x1=$\sqrt{6}$,x2=-$\sqrt{6}$ | D. | x1=3$\sqrt{2}$,x2=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )
如图,是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )| A. | 24cm | B. | 12cm | C. | 10cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{33}{6}$ | B. | $\frac{35}{6}$ | C. | 12 | D. | $\frac{37}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
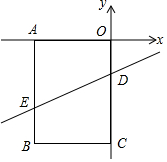 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$).
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com