
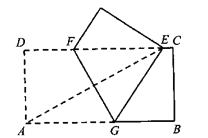
【题目】如图,矩形纸片ABCD中,AD= 1,AB一2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点仪当触ED的外接圆与BC相切于BC的中点N.则折痕FG的长为________
【答案】![]()
【解析】试题解析:设AE与FG的交点为O.
根据轴对称的性质,得AO=EO.
取AD的中点M,连接MO.
则MO=![]() DE,MO∥DC.
DE,MO∥DC.
设DE=x,则MO=![]() x,
x,
在矩形ABCD中,∠C=∠D=90°,
∴AE为△AED的外接圆的直径,O为圆心.
延长MO交BC于点N,则ON∥CD.
∴∠CNM=180°-∠C=90°.
∴ON⊥BC,四边形MNCD是矩形.
∴MN=CD=AB=2.∴ON=MN-MO=2-![]() x.
x.
∵△AED的外接圆与BC相切,
∴ON是△AED的外接圆的半径.
∴OE=ON=2-![]() x,AE=2ON=4-x.
x,AE=2ON=4-x.
在Rt△AED中,AD2+DE2=AE2,
∴12+x2=(4-x)2.
解这个方程,得x=![]() .
.
∴DE=![]() ,OE=2-
,OE=2-![]() x=
x=![]() .
.
根据轴对称的性质,得AE⊥FG.
∴∠FOE=∠D=90°.可得FO=![]() .
.
又AB∥CD,∴∠EFO=∠AGO,∠FEO=∠GAO.
∴△FEO≌△GAO.∴FO=GO.
∴FG=2FO=![]() .
.
∴折痕FG的长是![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点A、B、C在同一条直线上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点.
(1)画出符合题意的图形;
(2)依据(1)的图形,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台组织知识竞赛,共设20道选择题,每题必答,如表记录了3个参赛者的得分情况.
(1)参赛者小婷得76分,她答对了几道题?
(2)参赛者小明说他得了80分.你认为可能吗?为什么?
参赛者 | 答对题数 | 答错题数 | 总得分 |
甲 | 20 | 0 | 100 |
乙 | 19 | 1 | 94 |
丙 | 14 | 6 | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=(x﹣1)2﹣2图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是( )
A.(2,0)B.(﹣2,0)C.(1,0)D.(0,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=3,OB=5,点D为y轴上一点,其坐标为(0,1),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.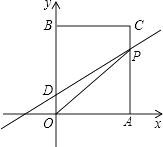
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②当点D关于OP的对称点落在x轴上时,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com