练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，△ABC内接于圆O，若圆的半径是$\frac{5}{2}$，AB=3，求tanC的值．

    分析 作直径AD，连接BD，根据圆周角定理得出∠ACB=∠ADB，在Rt△ABD中，求出∠ADB的正弦值即可．

    解答 解：作直径AD，连接BD，
    ∵∠ACB和∠ADB都对弧AB，
    ∴∠ACB=∠ADB，
    ∵圆的半径是$\frac{5}{2}$，
    ∴AD=5，
    ∵AD为直径，
    ∴∠ABD=90°，
    ∴BD=$\sqrt{A{D}^{2}-A{B}^{2}}$=4，
    ∴tanC=tanD=$\frac{AB}{BD}$=$\frac{3}{4}$．

    点评 本题考查了圆周角定理，三角形的外接圆和外心，解直角三角形的应用，关键是构造直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．如图△ABC，△DMN中∠A=∠MDN=90°，AB=AC=4，D为BC边中点，绕D点转动△DMN．使得DM与线段AB交于E点（不与A、B重合），DN边与线段AC交于F点
    （1）求证：DE=DF；
    （2）△DMN转动过程中，判断四边形AEDF的面积是否变化？若不变，请说明理由；
    （3）△DMN转动过程中，判断△DEF的面积有没有最大或最小值？若有求出此时的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，已知O是坐标原点，B、C两点的坐标分别为（3，-1），（2，1）．
    （1）以O点为位似中心在y轴左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；
    （2）如果△OBC内部一点M的坐标为（x，y），写出B、C、M对应点B′，C′，M′坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，在高出海平面100m的悬崖顶A处，观测海面上的一艘小船B，并测得它的俯角为30°，则船与观测者之间的水平距离是100$\sqrt{3}$m．（结果保留要有号，不取近似值）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．将二次函数y=2x2的图象向左平移2个单位，得到的新图象对应的函数表达式为（　　）
    A．y=2x2+2B．y=2（x+2）2C．y=2x2-2D．y=2（x-2）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，在Rt△ABC中∠ACB=90°，斜边上的中线CF=8cm，DE是△ABC的中位线，则下列叙述中，正确的序号为（　　）
    ①S△ACF=S△BCF；②DE=8cm；③四边形CDFE是矩形；④S△ABC=2S△CDE．
    A．①②④B．①③④C．②③④D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

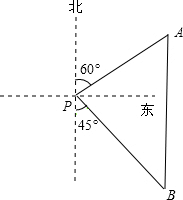    2．如图，一艘海轮位于灯塔P的北偏东60°方向，距灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，此时B处距离灯塔P有多远（结果取整数）．参考数值：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，$\sqrt{6}$≈2.4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．以下各组线段为边不能组成三角形的是（　　）
    A．4，3，3B．1，5，6C．2，5，4D．5，8，4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．某商人在一次买卖中均以180元卖出两件衣服，一件赚25%，一件赔25%，在这次交易中，该商人（　　）
    A．赚24元B．赔24元C．不赚不赔D．无法确定

    查看答案和解析>>

    同步练习册答案