
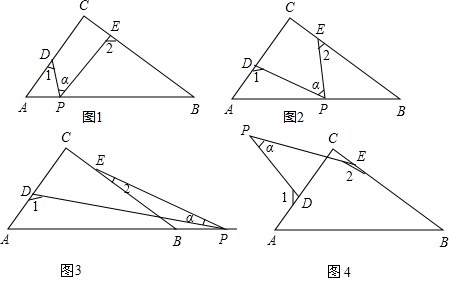
分析 (1)如图1中,连接PC.由∠1=∠3+∠DPC,∠2=∠4+∠CPE,推出∠1+∠2=(∠DPC+∠CPE)+(∠3+∠4)=∠α+90°=130°;
(2)结论:∠1+∠2=90°+∠α.连接PC.由∠1=∠3+∠DPC,∠2=∠4+∠CPE,推出∠1+∠2=(∠DPC+∠CPE)+(∠3+∠4)=90°+∠α;
(3)如图3中,结论:∠1-∠2-∠α=90°.由∠1=∠3+∠C,∠3=∠α+∠2,推出∠1=∠α+∠2+90°,即∠1-∠2-∠α=90°;
(4)如图4中,结论:∠1+∠2-∠α=270°.由∠1=∠α+∠3,∠3=∠C+∠PEC,∠PEC=180°-∠2,推出∠1=∠α+∠C+180°-∠2,推出∠1=∠α+90°+180°-∠2,即∠1+∠2-∠α=270°;
解答 解:(1)如图1中,连接PC.
∵∠1=∠3+∠DPC,∠2=∠4+∠CPE,
∴∠1+∠2=(∠DPC+∠CPE)+(∠3+∠4)=∠α+90°=130°,
故答案为130;
(2)如图2中,结论:∠1+∠2=90°+∠α.理由如下:
连接PC.
∵∠1=∠3+∠DPC,∠2=∠4+∠CPE,
∴∠1+∠2=(∠DPC+∠CPE)+(∠3+∠4)=90°+∠α;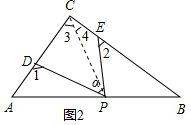
(3)如图3中,结论:∠1-∠2-∠α=90°.
理由:∵∠1=∠3+∠C,∠3=∠α+∠2,
∴∠1=∠α+∠2+90°,
∴∠1-∠2-∠α=90°.
故答案为∠1-∠2-∠α=90°;
(4)如图4中,结论:∠1+∠2-∠α=270°.
理由:∵∠1=∠α+∠3,∠3=∠C+∠PEC,∠PEC=180°-∠2,
∴∠1=∠α+∠C+180°-∠2,
∴∠1=∠α+90°+180°-∠2,
∴∠1+∠2-∠α=270°.
故答案为∠1+∠2-∠α=270°;
点评 本题考查三角形综合题、三角形的外角的性质,三角形内角和定理等知识,解题的关键是学会添加常用辅助线,灵活运用三角形的外角等于不相邻的两个内角之和解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | y=3(x+3)2-2 | B. | y=3(x+3)2+2 | C. | y=3(x+2)2+3 | D. | y=3(x-2)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 红丝带是关注艾滋病防止问题的国际性标志,人们将等宽红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,图中红丝带重叠部分形成的图形一定是菱形.
红丝带是关注艾滋病防止问题的国际性标志,人们将等宽红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,图中红丝带重叠部分形成的图形一定是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com