
【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.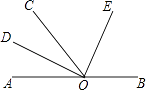
(1)∠AOD的余角是 , ∠COD的余角是
(2)OE是∠BOC的平分线吗?请说明理由.
【答案】
(1)∠COE、∠BOE;∠COE、∠BOE
(2)
解:OE平分∠BOC,
理由:∵∠DOE=90°,
∴∠AOD+∠BOE=90°,
∴∠COD+∠DOE=90°,
∴∠AOD+∠BOE=∠COD+∠DOE
∵OD平分∠AOC,
∴∠AOD=∠COD,
∴∠COE=∠BOE
∴OE平分∠BOC
【解析】解:(1)∵OD平分∠AOC,
∴∠AOD=∠COD,
∵∠DOE=90°,
∴∠DOC+∠COE=90°,∠AOD+∠BOE=90°,
∴∠AOD+∠COE=90°,
∴∠AOD的余角是:∠COE、∠BOE;
∠COD的余角是:∠COE,∠BOE;
故答案为:∠COE,∠BOE;∠COE,∠BOE;
(1)直接利用角平分线的定义得出∠AOD=∠COD,进而利用已知得出∠AOD、∠COD的余角;(2)利用(1)中所求得出OE是∠BOC的平分线.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
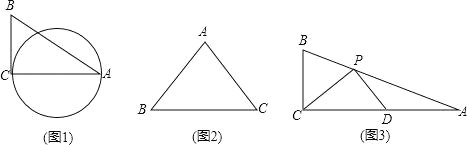
(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
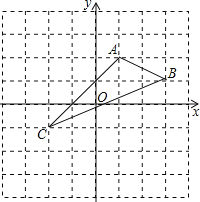
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)写出A1,B1,C1的坐标(直接写出答案),A1 ;B1 ;C1 .
(3)△ A1B1C1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,∠AOB=60°,OC平分∠AOB,C为角平分线上一点,过点C作CD⊥OC,垂足为C,交OB于点D,CE∥OA交OB于点E.判断△CED的形状,并说明理由.
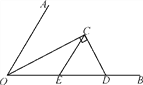
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.多边形的内角和为360°
B.若2a﹣b=1,则代数式6a﹣3b﹣3=0
C.二次函数y=(x﹣1)2+2的图象与y轴的交点的坐标为(0,2)
D.矩形的对角线互相垂直平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达。已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:①在数轴上,原点两旁的两个点所表示的数都是互为相反数;②任何正数必定大于它的倒数;③5ab, ![]() ,
, ![]() 都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com