
【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.

(1)求证:△BDF≌△CDE;
(2)若AB=AC,求证:四边形BFCE是菱形.
【答案】(1)△BDF≌△EDC;(2)四边形BFCE是菱形.
【解析】试题分析:(1)由CE、BF的内错角相等,可得出△CED和△BFD的两组对应角相等;已知D是BC的中点,即BD=DC,由AAS即可证得两三角形全等;
(2)若AB=AC,则△ABC是等腰三角形,而D是底边BC的中点,根据等腰三角形三线合一的性质可证得AD⊥BC;由(1)的全等三角形,易证得四边形BFCE的对角线互相平分;根据对角线互相垂直平分的四边形是菱形即可判定四边形BFCE是菱形.
试题解析:(1)∵CE∥BF,
∴∠ECD=∠FBD,∠DEC=∠DFB;
又∵D是BC的中点,即BD=DC,
∴△BDF≌△EDC(AAS)
(2)∵AB=AC,
∴△ABC是等腰三角形;
又∵BD=DC,∴AD⊥BC(三线合一),
由(1)知:△BDF≌△EDC,
则DE=DF,DB=DC;
∴四边形BFCE是菱形(对角线互相平分且互相垂直的四边形为菱形).


科目:初中数学 来源: 题型:
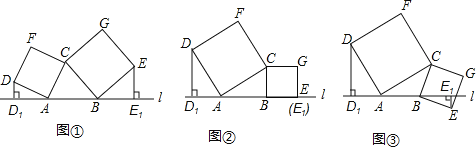
【题目】如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某一周某种股票每天的收盘价(收盘价:股票每天交易结束时的价格)

(1)填表,并回答哪天收盘价最高?哪天收盘价最低?
(2)最高价与最低价相差多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c是△ABC的三条边长,化简|a+b﹣c|+|b﹣a﹣c|的结果为( )
A.2a+2bB.2a+2b﹣2cC.2b﹣2cD.2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2011个格子中的数为 ( )
![]()
A. 3 B. 2 C. 0 D. -1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com