
 S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.
S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.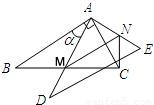
 MN•CN,而MC=4-x,故利用相似三角形的对应边成比例用含x的代数式表示出CN,就可求得S△MNC的函数关系式.
MN•CN,而MC=4-x,故利用相似三角形的对应边成比例用含x的代数式表示出CN,就可求得S△MNC的函数关系式. S△ABC时,求得x的值,讨论x取不同值时直线AD与⊙N的位置关系.
S△ABC时,求得x的值,讨论x取不同值时直线AD与⊙N的位置关系.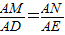 ,
,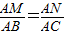 ,
,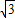 ,
, ,
,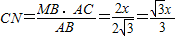 ,
, CM•CN=
CM•CN= (4-x)•
(4-x)• x=
x= (4x-x2)(0<x<4).
(4x-x2)(0<x<4). ,∴AM=MB.
,∴AM=MB. BC=2,即x=2.
BC=2,即x=2.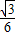 (4x-x2)=
(4x-x2)=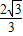 ,∵S△ABC=
,∵S△ABC= AB•AC=2
AB•AC=2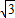 ,
, S△ABC.
S△ABC. S△ABC时
S△ABC时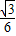 (4x-x2)=
(4x-x2)=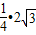 解得x=1或x=3.
解得x=1或x=3. =
=
 ,即AN>NC,
,即AN>NC,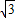 ,MC=1,MN=2,AN=1
,MC=1,MN=2,AN=1

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《四边形》(10)(解析版) 题型:解答题
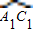 与OB1相交于点B2,设正方形OA1B1C1与扇形OA1C1之间的阴影部分的面积为S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2,
与OB1相交于点B2,设正方形OA1B1C1与扇形OA1C1之间的阴影部分的面积为S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2,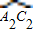 与OB1相交于点B3,设正方形OA2B2C2与扇形OA2C2之间的阴影部分面积为S2;按此规律继续作下去,设正方形OAnBnCn与扇形OAnCn之间的阴影部分面积为Sn.
与OB1相交于点B3,设正方形OA2B2C2与扇形OA2C2之间的阴影部分面积为S2;按此规律继续作下去,设正方形OAnBnCn与扇形OAnCn之间的阴影部分面积为Sn.
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《相交线与平行线》(02)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
 x2+bx(b为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
x2+bx(b为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2008年湖南省邵阳市中考数学试卷(解析版) 题型:填空题
 (2008•邵阳)如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BD,BC,AB=5,AC=4,则BD= .
(2008•邵阳)如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BD,BC,AB=5,AC=4,则BD= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com