
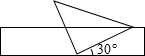
 将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为
将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为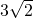 cm
cm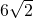 cm
cm科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:044
我们知道:由于圆是中心对称图形有,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1)。

探索下列问题:
(
1)在图2给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意直线),将每个正方形都分割成面积相等的两部分;
(2
)一条竖直方向的直线m以及任意直线n,在由左向右平移的过程中,将六边形分成左右两部分,其面积分别记为S1和S2。① 你在图3中相应图形下方的横线上分别填写S1与S2的数量关系式(用摚紨,摚綌,摚緮连接);
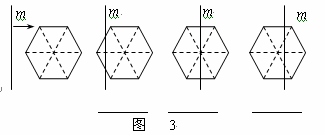
② 请你在图4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用摚紨,摚綌,摚緮连接)。

(3
)是否存在一条直线,将一个任意平面图形(如图11-5)分割成面积相等的两部分?请简略说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
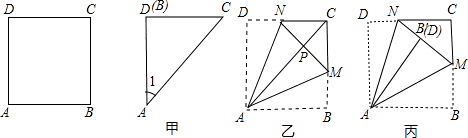
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com