
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
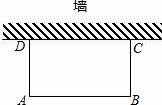
解:(1)设所围矩形ABCD的长AB为x米,则宽AD为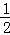 (80﹣x)米(1分).
(80﹣x)米(1分).
(说明:AD的表达式不写不扣分).
依题意,得x•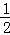 (80﹣x)=750(2分).
(80﹣x)=750(2分).
即,x2﹣80x+1500=0,
解此方程,得x1=30,x2=50(3分).
∵墙的长度不超过45m,∴x2=50不合题意,应舍去(4分).
当x=30时,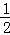 (80﹣x)=
(80﹣x)=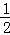 ×(80﹣30)=25,
×(80﹣30)=25,
所以,当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2(5分).
(2)不能.
因为由x•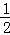 (80﹣x)=810得x2﹣80x+1620=0(6分).
(80﹣x)=810得x2﹣80x+1620=0(6分).
又∵b2﹣4ac=(﹣80)2﹣4×1×1620=﹣80<0,
∴上述方程没有实数根(7分).
因此,不能使所围矩形场地的面积为810m2(8分).
说明:如果未知数的设法不同,或用二次函数的知识解答,只要过程及结果正确,请参照给分.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为()
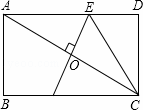
A. 3 B. 3.5 C. 2.5 D. 2.8
查看答案和解析>>
科目:初中数学 来源: 题型:
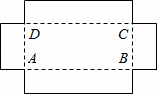
如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为xcm.
(1)底面的长AB=cm,宽BC=cm(用含x的代数式表示)
(2)当做成盒子的底面积为300cm2时,求该盒子的容积.
(3)该盒子的侧面积S是否存在最大的情况?若存在,求出x的值及最大值是多少?若不存在,说明理由.
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com