
【题目】数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
(1) (思想应用)已知m, n均为正实数,且m+n=2求![]() 的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
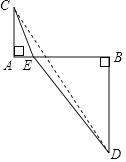
①用含m的代数式表示CE=_______, 用含n的代数式表示DE= ;
②据此求![]() 的最小值;
的最小值;
(2)(类比应用)根据上述的方法,求代数式![]() 的最小值.
的最小值.
【答案】(1)①![]() ,
,![]() ;②
;②![]() ;(2)20.
;(2)20.
【解析】
(1)①利用勾股定理得到CE=![]() ,DE=
,DE=![]() ;
;
②根据CE+DE=![]() +
+![]() ,利用两点之间线段得到CE+DE≥CD(当且仅当C、E、D共线时取等号),作DH⊥CA交CA的延长线于H,如图,易得四边形ABDH为矩形,利用勾股定理计算出CD=
,利用两点之间线段得到CE+DE≥CD(当且仅当C、E、D共线时取等号),作DH⊥CA交CA的延长线于H,如图,易得四边形ABDH为矩形,利用勾股定理计算出CD=![]() ,从而求解;
,从而求解;
(2)如(1)中图,设AB=16,CA=5,BD=7,AE=x,则BE=16-x,利用勾股定理得到CE=![]() ,DE=
,DE=![]() ;根据两点之间线段得到而CE+DE≥CD(当且仅当C、E、D共线时取等号),根据四边形ABDH为矩形,利用勾股定理计算出CD即可得到最小值.
;根据两点之间线段得到而CE+DE≥CD(当且仅当C、E、D共线时取等号),根据四边形ABDH为矩形,利用勾股定理计算出CD即可得到最小值.
解:(1)①在Rt△ACE中,![]() ,
,
在Rt△BDE中,DE=![]() ;
;
②CE+DE=![]() +
+![]() ,
,
而CE+DE≥CD(当且仅当C、E、D共线时取等号),
作DH⊥CA交CA的延长线于H,如图,易得四边形ABDH为矩形,
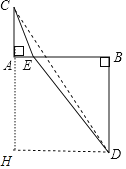
∴AH=BD=2,DH=AB=2,
在Rt△CHD中,CD=![]() ,
,
∴CE+DE的最小值为![]() ,即
,即![]() 的最小值为
的最小值为![]() ;
;
(2)如(1)中图,设AB=16,CA=5,BD=7,AE=x,则BE=16-x,
在Rt△ACE中,CE=![]() ,
,
在Rt△BDE中,DE=![]()
∴CE+DE=![]() +
+![]() ,
,
而CE+DE≥CD(当且仅当C、E、D共线时取等号),
∵四边形ABDH为矩形,
∴AH=BD=7,DH=AB=16,
在Rt△CHD中,CD=![]()
∴CE+DE的最小值为20,即![]() 的最小值为20.
的最小值为20.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
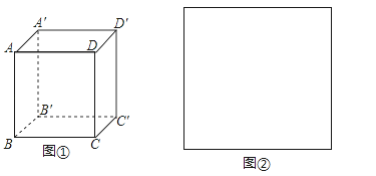
(1)写出与棱AB平行的所有的棱;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个无人超市仓库的货物搬运工作全部由机器人![]() 和机器人
和机器人![]() 完成,工作记录显示机器人
完成,工作记录显示机器人![]() 比机器人
比机器人![]() 每小时多搬运50件货物.机器人
每小时多搬运50件货物.机器人![]() 搬运2000件货物与机器人
搬运2000件货物与机器人![]() 搬运1600件货物所用的时间相等,则机器人
搬运1600件货物所用的时间相等,则机器人![]() 每小时搬运货物( )
每小时搬运货物( )
A.250件B.200件C.150件D.100件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,解决问题:
网约车、滴滴打车、共享汽车等新的出行方式越来越受大众欢迎.如图1,是某种网约车的计价规则,车辆行驶![]() ,平均速度为
,平均速度为![]() ,则打车费用为
,则打车费用为![]() 元(不足
元(不足![]() 元按
元按 ![]() 元计价).某日,小明出行时叫了一辆网约车,按上述计价规则,打车费用
元计价).某日,小明出行时叫了一辆网约车,按上述计价规则,打车费用![]() (元)与行驶里程
(元)与行驶里程![]() 的函数关系如图 2 所示.
的函数关系如图 2 所示.
(1)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)若![]() ,求该车行驶的平均速度.
,求该车行驶的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
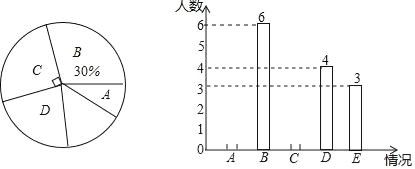
【题目】随着初三的到来,同学们都进入紧张的初三冲刺阶段,为了了解年级同学们每天作业完成时间情况,现对年级部分同学进行调查统计,并制成如下两幅不完整的统计图:(其中A代表完成作业时间2小时,B代表完成作业时间2.5小时,C代表完成作业时间3小时,D代表睡眠时间3.5小时,E代表睡眠时间4小时),其中扇形统计图中“C”的圆心角为90°,请你结合统计图所给信息解答下列问题:
(1)共抽取了 名同学进行调查,同学们的完成作业时间的中位数是 小时,并将条形统计图补充完整;
(2)抽取调查的同学中,D类学生有两男两女,E类学生有两男一女,现要从D、E两类学生中各抽取一名同学,了解其每天晚上作业时间安排的具体情况,则抽取到的两名学生刚好是一男一女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等边三角形,点D是AC边上动点,∠CBD=α,把△ABD沿BD对折,A对应点为A'.
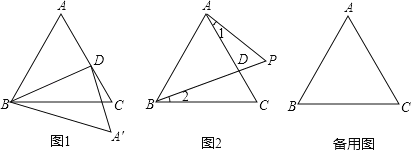
(1)①当α=15°时,∠CBA'= ;
②用α表示∠CBA'为 .
(2)如图2,点P在BD延长线上,且∠1=∠2=α.
①当0°<α<60°时,试探究AP,BP,CP之间是否存在一定数量关系,猜想并说明理由.
②BP=8,CP=n,则CA'= .(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=45°,O为BC中点,如果点M、N分别在线段AB、AC上移动,设AM的长为x,CN的长为y,且x、y满足等式![]() (a>0)
(a>0)
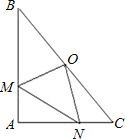
(1)求证:BM=AN;
(2)请你判断△OMN的形状,并证明你的结论;
(3)求证:当OM∥AC时,无论a取何正数,△OMN与△ABC面积的比总是定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.
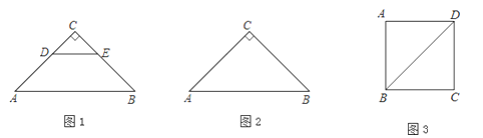
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为![]() , 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
, 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com