
| A. | x≥-1 | B. | x≤-1 | C. | x≥4 | D. | x≤4 |
科目:初中数学 来源: 题型:选择题
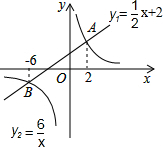 如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点,则当y1<y2时,x的取值范围是( )
如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点,则当y1<y2时,x的取值范围是( )| A. | x<-6或x>2 | B. | -6<x<0或x>2 | C. | x<-6或0<x<2 | D. | -6<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
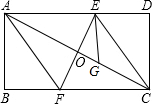 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE;过点E作EG⊥AD交AC于点G.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE;过点E作EG⊥AD交AC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知反比例函数y=$\frac{6}{x}$.
已知反比例函数y=$\frac{6}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 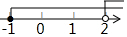 | B. | 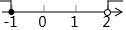 | C. | 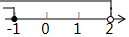 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
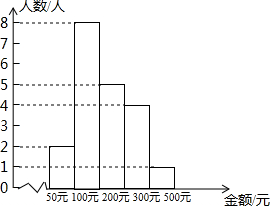 某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论错误的是( )
某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论错误的是( )| A. | 样本中位数是200元 | |
| B. | 样本容量是20 | |
| C. | 该企业员工捐款金额的平均数是180元 | |
| D. | 该企业员工最大捐款金额是500元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com