
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在![]() 轴上.
轴上.
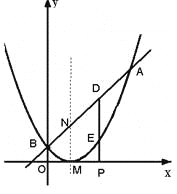
(1)求m的值及这个二次函数的解析式;
(2)若P(![]() ,0) 是
,0) 是![]() 轴上的一个动点,过P作
轴上的一个动点,过P作![]() 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<![]() < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
【答案】(1) ![]() ;
;![]() (2)①
(2)①![]() 有最大值
有最大值![]() ②存在.(2,0)(
②存在.(2,0)(![]() ,0)(
,0)(![]() ,0).
,0).
【解析】
(1)将A点坐标分别代入抛物线的直线,便可求出抛物线的解析式和m的值;
(2)过A作AH⊥PM于H,利用△MAB的面积=S梯形BOHA-S△BOM-S△AMH计算即可;
(3)①线段DE的长为h,根据P点坐标分别求出DE两点坐标,便可求出h与a之间的函数关系式,进而可求出线段DE的最大值;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,要使四边形NMED是平行四边形,必须DE=MN=2,由①知DE=|-a2+3a|,进而求出a的值,所以P的坐标可求出.
(1)设抛物线的解析式为y=a(x-1)2,
∵点A(3,4)在抛物线上,则4=a(3-1)2,
解得a=1,
∴抛物线的解析式为y=(x-1)2
∵点A(3,4)也在直线y=x+m,即4=3+m,
解得m=1;
(2)过A作AH⊥PM于H,
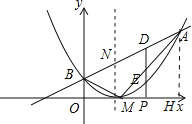
∵B(0,1),M(1,0),A(3,4),
∴OB=1,OH=3,AH=4,
∴△MAB的面积=S梯形BOHA-S△BOM-S△AMH=7.5-![]() ×1×1-
×1×1-![]() ×2×4=3;
×2×4=3;
(3)①已知P点坐标为P(a,0),则E点坐标为E(a,a2-2a+1),D点坐标为D(a,a+1),
h=DE=yD-yE=a+1-(a2-2a+1)=-a2+3a,
∴h与a之间的函数关系式为h=-a2+3a=-(a-![]() )2+
)2+![]() (0<a<3),
(0<a<3),
∴线段DE的最大值是![]() ;
;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,
理由是∵M(1,0),
∴把x=1代入y=x+1得:y=2,
即N(1,2),
∴MN=2,
要使四边形NMED是平行四边形,必须DE=MN=2,
由①知DE=|-a2+3a|,
∴2=|-a2+3a|,
解得:a1=2,a2=1,a3=![]() ,a4=
,a4=![]() ,
,
∴(2,0),(1,0)(因为和M重合,舍去)(![]() ,0),(
,0),(![]() ,0)
,0)
∴P的坐标是(2,0),(![]() ,0),(
,0),(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AE是△ABC的角平分线.AE的垂直平分线交AB于点O,以点O为圆心,OA为半径作⊙O,交AB于点F.
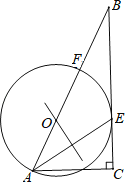
(1)求证:BC是⊙O的切线;
(2)若AC=2,tanB![]() ,求⊙O的半径r的值.
,求⊙O的半径r的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米/秒的速度自A点出发沿AB方向运动,动点Q以2厘米/秒的速度自B点出发沿BC方向运动至C点停止,同时P点也停止运动若点P,Q同时出发运动了t秒,记△BPQ的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是( )
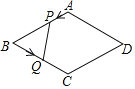
A.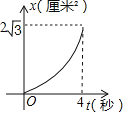 B.
B.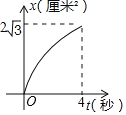
C.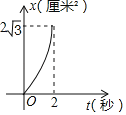 D.
D.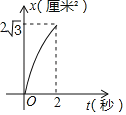
查看答案和解析>>
科目:初中数学 来源: 题型:
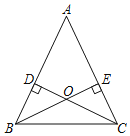
【题目】如图,锐角三角形ABC的两条高线BE、CD相交于点O,BE=CD.
(1)求证:BD=CE;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
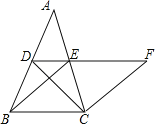
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
(1)求证:四边形BCFE是菱形;
(2)在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).
查看答案和解析>>
科目:初中数学 来源: 题型:
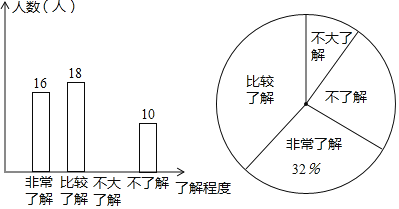
【题目】某校为了解学生对“第二十届中国哈尔滨冰雪大世界”主题景观的了解情况,在全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图的不完整的两幅统计图:
(1)本次调查共抽取了多少名学生;
(2)通过计算补全条形图;
(3)若该学校共有![]() 名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
.
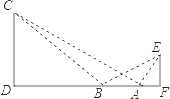
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(﹣2,﹣2),B(0,3),C(3,3),D(4,﹣2),y是关于x的二次函数,抛物线y1经过点A、B、C,抛物线y2经过点B、C、D,抛物线y3经过点A、B、D,抛物线y4经过点A、C、D.下列判断:
①四条抛物线的开口方向均向下;
②当x<0时,至少有一条抛物线表达式中的y均随x的增大而减小;
③抛物线y1的顶点在抛物线y2顶点的上方;
④抛物线y4与y轴的交点在点B的上方.
所有正确结论的序号为_____.
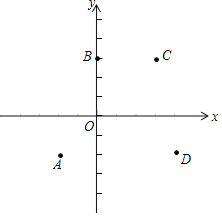
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() 与x轴交于A,C(A在C的左侧),点B在抛物线上,其横坐标为1,连接BC,BO,点F为OB中点.
与x轴交于A,C(A在C的左侧),点B在抛物线上,其横坐标为1,连接BC,BO,点F为OB中点.
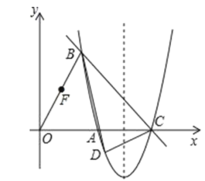
(1)求直线BC的函数表达式;
(2)若点D为抛物线第四象限上的一个动点,连接BD,CD,点E为x轴上一动点,当△BCD的面积的最大时,求点D的坐标,及|FE﹣DE|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com