
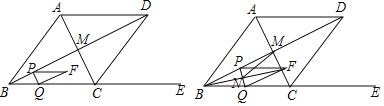
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点M,已知BC=5,点E在射线BC上,tan∠DCE=![]() ,点P从点B出发,以每秒2
,点P从点B出发,以每秒2![]() 个单位沿BD方向向终点D匀速运动,过点P作PQ⊥BD交射线BC于点O,以BP、BQ为邻边构造PBQF,设点P的运动时间为t(t>0).
个单位沿BD方向向终点D匀速运动,过点P作PQ⊥BD交射线BC于点O,以BP、BQ为邻边构造PBQF,设点P的运动时间为t(t>0).
(1)tan∠DBE= ;
(2)求点F落在CD上时t的值;
(3)求PBQF与△BCD重叠部分面积S与t之间的函数关系式;
(4)连接PBQF的对角线BF,设BF与PQ交于点N,连接MN,当MN与△ABC的边平行(不重合)或垂直时,直接写出t的值.
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)见解析;(4)t的值为
;(3)见解析;(4)t的值为![]() 或
或![]() 或
或![]() 或2.
或2.
【解析】
(1)如图1中,作DH⊥BE于H.解直角三角形求出BH,DH即可解决问题.
(2)如图2中,由PF∥CB,可得![]() ,由此构建方程即可解决问题.
,由此构建方程即可解决问题.
(3)分三种情形:如图3-1中,当![]() 时,重叠部分是平行四边形PBQF.如图3-2中,当
时,重叠部分是平行四边形PBQF.如图3-2中,当![]() 时,重叠部分是五边形PBQRT.如图3-3中,当1<t≤2时,重叠部分是四边形PBCT,分别求解即可解决问题.
时,重叠部分是五边形PBQRT.如图3-3中,当1<t≤2时,重叠部分是四边形PBCT,分别求解即可解决问题.
(4)分四种情形:如图4-1中,当MN∥AB时,设CM交BF于T.如图4-2中,当MN⊥BC时.如图4-3中,当MN⊥AB时.当点P与点D重合时,MN∥BC,分别求解即可.
解:(1)如图1中,作DH⊥BE于H.
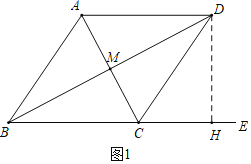
在Rt△BCD中,∵∠DHC=90°,CD=5,tan∠DCH=![]() ,
,
∴DH=4,CH=3,
∴BH=BC+CH=5+3=8,
∴tan∠DBE=![]() =
=![]() =
=![]() .
.
故答案为![]() .
.
(2)如图2中,
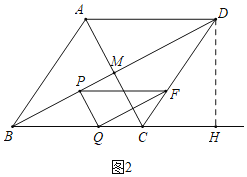
∵四边形ABCD是菱形,
∴AC⊥BD,
∵BC=5,tan∠CBM=![]() =
=![]() ,
,
∴CM=![]() ,BM=DM=2
,BM=DM=2![]() ,
,
∵PF∥CB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() .
.
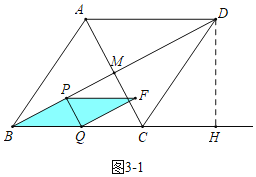
(3)如图3﹣1中,当0<t≤![]() 时,重叠部分是平行四边形PBQF,S=PBPQ=2
时,重叠部分是平行四边形PBQF,S=PBPQ=2![]() t
t![]() t=10t2.
t=10t2.
如图3﹣2中,当![]() <t≤1时,重叠部分是五边形PBQRT,S=S平行四边形PBQF﹣S△TRF=10t2﹣
<t≤1时,重叠部分是五边形PBQRT,S=S平行四边形PBQF﹣S△TRF=10t2﹣![]() [2
[2![]() t﹣(5﹣5t)]
t﹣(5﹣5t)]![]() [2
[2![]() t﹣(5﹣5t)]=﹣55t2+(20
t﹣(5﹣5t)]=﹣55t2+(20![]() +50)t﹣25.
+50)t﹣25.
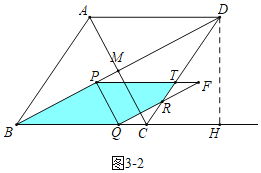
如图3﹣3中,当1<t≤2时,重叠部分是四边形PBCT,S=S△BCD﹣S△PDT=![]() ×5×4﹣
×5×4﹣![]() (5﹣
(5﹣![]() t)(4﹣2t)=﹣
t)(4﹣2t)=﹣![]() t2+10t.
t2+10t.
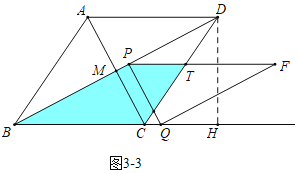
(4)如图4﹣1中,当MN∥AB时,设CM交BF于T.

∵PN∥MT,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴MT=![]() ,
,
∵MN∥AB,
∴![]() =
=![]() =
=![]() =2,
=2,
∴PB=![]() BM,
BM,
∴2![]() t=
t=![]() ×2
×2![]() ,
,
∴t=![]() .
.
如图4﹣2中,当MN⊥BC时,易知点F落在DH时,
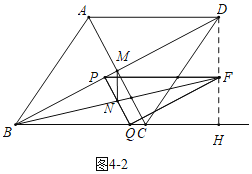
∵PF∥BH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() .
.
如图4﹣3中,当MN⊥AB时,易知∠PNM=∠ABD,
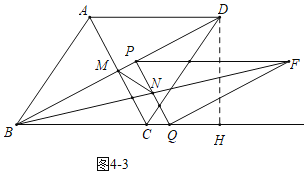
可得tan∠PNM=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ,
,
当点P与点D重合时,MN∥BC,此时t=2,
综上所述,满足条件的t的值为![]() 或
或![]() 或
或![]() 或2.
或2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
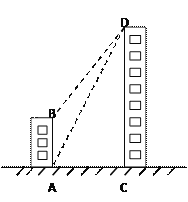
【题目】如图,一栋居民楼AB的高为16米,远处有一栋商务楼CD,小明在居民楼的楼底A处测得商务楼顶D处的仰角为![]() ,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为
,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为![]() .其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
.其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
(参考数据: ![]() ,
, ![]() .结果精确到0.1米)
.结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() (如图),点
(如图),点![]() ,
,![]() 分别为射线
分别为射线![]() 上的动点(点C、E都不与点B重合),连接AC、AE使得
上的动点(点C、E都不与点B重合),连接AC、AE使得![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
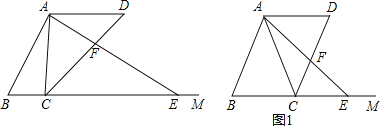
(1)如图1,当![]() 时,求AF的长.
时,求AF的长.
(2)当点![]() 在点
在点![]() 的右侧时,求
的右侧时,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.
(3)连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,直接写出
是等腰三角形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
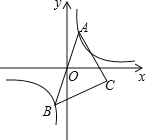
【题目】如图,已知点A是双曲线y=![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() (k<0)上运动,则k的值是_____.
(k<0)上运动,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意:B级满意;C级:基本满意:D级:不满意),并将调查结果绘制成如两幅不完整的统计图,请根据统计图中的信息解决下列问题:
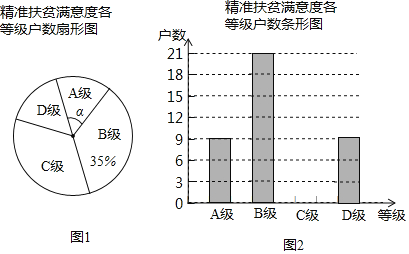
(1)本次抽样调查测试的建档立卡贫困户的总户数是 ;
(2)图①中,∠α的度数是 ,并把图②条形统计图补充完整;
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的户数约为多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
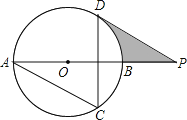
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
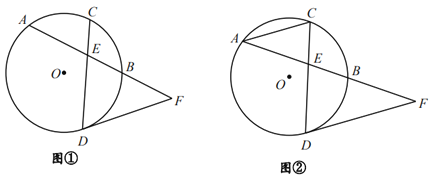
【题目】如图,已知,⊙O的半径![]() ,弦AB,CD交于点E,C为
,弦AB,CD交于点E,C为![]() 的中点,过D点的直线交AB延长线与点F,且DF=EF.
的中点,过D点的直线交AB延长线与点F,且DF=EF.
(1)如图①,试判断DF与⊙O的位置关系,并说明理由;
(2)如图②,连接AC,若AC∥DF,BE=![]() AE,求CE的长.
AE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化课改,落实立德树人目标,某学校设置了以下四门拓展性课程:A.数学思维,B.文学鉴赏,C.红船课程,D.3D打印,规定每位学生选报一门.为了解学生的报名情况,随机抽取了部分学生进行调查,并制作成如下两幅不完整的统计图,请回答下列问题:
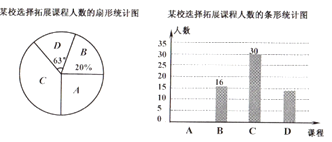
(1)求这次被调查的学生人数;
(2)请将条形统计图补充完整;
(3)假如全校有学生1000人,请估计选报“红船课程”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com