
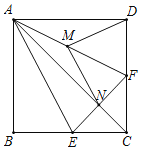
【题目】操作与证明:如图,把一个含![]() 角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、
角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、![]() 其中AC与EF交于点N,取AF中点M,连接MD、MN.
其中AC与EF交于点N,取AF中点M,连接MD、MN.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 在
在![]() 的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据正方形性质得:AB=AD=BC=CD,∠ABE=∠ADF=90°,再根据等腰直角三角形得BE=DF,证明△ABE≌△ADF,得AE=AF,则△AFE是等腰三角形;
(2)先根据直角三角形斜边中线等于斜边一半得:DM=![]() AF,再由等腰三角形三线合一得:AC⊥EF,EN=FN,同理MN=
AF,再由等腰三角形三线合一得:AC⊥EF,EN=FN,同理MN=![]() AF,则DM=MN;可证∠FMD=2∠FAD,∠FMN==2∠FAC,
AF,则DM=MN;可证∠FMD=2∠FAD,∠FMN==2∠FAC,
则∠DMN=∠DMF+∠FMN=2∠FAD +2∠FAC=2∠DAC=90°.即可得到DM⊥MN.
(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠ABE=∠ADF=90°,
∵△EFC是等腰直角三角形,∴CE=CF,∴BE=DF,∴△ABE≌△ADF(SAS),∴AE=AF,∴△AFE是等腰三角形;
(2)DM=MN,且DM⊥MN.理由是:
在Rt△ADF中,∵M是AF的中点,∴DM=![]() AF,
AF,
∵EC=FC,AC平分∠ECF,
∴AC⊥EF,EN=FN,
∴∠ANF=90°,
∴MN=![]() AF,∴MD=MN.
AF,∴MD=MN.
由(1)得:△ABE≌△ADF,∴∠BAE=∠FAD,
∵DM=![]() AF=AM,∴∠FAD=∠ADM,
AF=AM,∴∠FAD=∠ADM,
∴∠FMD=∠FAD+∠ADM=2∠FAD,
同理:∠FMN==2∠FAC,
∴∠DMN=∠DMF+∠FMN=2∠FAD +2∠FAC=2∠DAC=2×45°=90°.
∴MD⊥MN.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,P是BC边上一动点,设BP=x,若能在AC边上找一点Q,使∠BQP=90°,则x的范围是 . 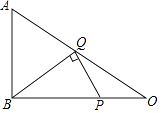
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s, 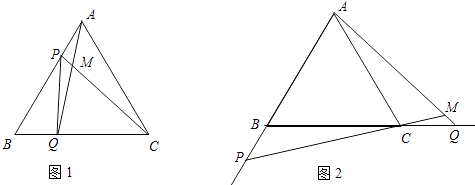
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)何时△PBQ是直角三角形?
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距200千米,一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,相向而行.已知客车的速度为60千米/小时,出租车的速度是100千米/小时.
(1)多长时间后两车相遇?
(2)若甲乙两地之间有相距50km的A、B两个加油站,当客车进入A站加油时,出租车恰好进入B站加油,求A加油站到甲地的距离.
(3)若出租车到达甲地休息10分钟后,按原速原路返回.出租车能否在到达乙地或到达乙地之前追上客车?若不能,则出租车往返的过程中,至少提速为多少才能在到达乙地或到达乙地之前追上客车?是否超速(高速限速为120千米/小时)?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,边长为1的正方形OAP1B的顶点A、B分别在x轴、y轴上,点P1在反比例函数y= ![]() (x>0)的图象上,过P1A的中点B1作矩形B1AA1P2 , 使顶点P2落在反比例函数的图象上,再过P2A1的中点B2作矩形B2A1A2P3 , 使顶点P3落在反比例函数的图象上,…,依此规律,作出矩形Bn﹣1An﹣2An﹣1Pn时,落在反比例函数图象上的顶点Pn的坐标是 .
(x>0)的图象上,过P1A的中点B1作矩形B1AA1P2 , 使顶点P2落在反比例函数的图象上,再过P2A1的中点B2作矩形B2A1A2P3 , 使顶点P3落在反比例函数的图象上,…,依此规律,作出矩形Bn﹣1An﹣2An﹣1Pn时,落在反比例函数图象上的顶点Pn的坐标是 . 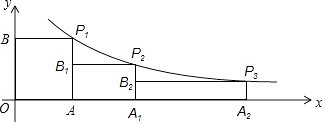
查看答案和解析>>
科目:初中数学 来源: 题型:
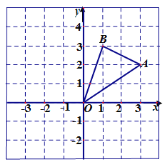
【题目】如图,在边长为1的正方形组成的网格中,三角形AOB的顶点均在格点上,A(3,2),B(1,3),
(1)将三角形AOB先向左平移3个单位长度,后向下平移1个单位得到三角形A1O1B1,请直接作出三角形A1O1B1;
(2)请直接写出三角形A1O1B1三个顶点的坐标;
(3)三角形A1O1B1的面积为_______平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
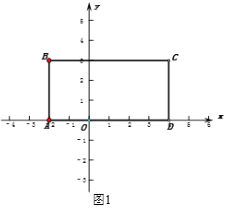
【题目】在平面直角坐标系中,如图1,第二象限内一点B(a,b),过B线段BA垂直于x轴,垂足为点A,实数a、b满足![]() ,D(4,0),将线段AB向右平移使点A和点D重合得到线段DC,连接BC与y轴相交于点M.
,D(4,0),将线段AB向右平移使点A和点D重合得到线段DC,连接BC与y轴相交于点M.
(1)求点C的坐标;
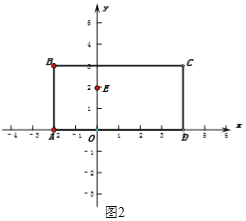
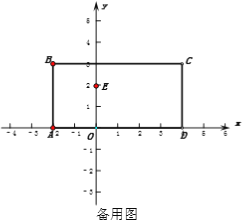
(2)如图2,动点P从A点出发,沿折线AB-BC运动,运动到点C即停止运动,速度为每秒2个单位长度,设运动时间为t秒,当点P运动至线段BC上时,请用含有t的代数式表示在这一运动过程中线段PM的长,并直接写出t的取值范围;
(3)在(2)的条件下,y轴上有一点E(0,2),在点P在折线AB-BC运动过程中是否存在t值,使三角形PBE的面积为2,若存在,求出t值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com