
【题目】已知直线y=kx+b与直线y=2x+1平行,且过点(1,﹣3).
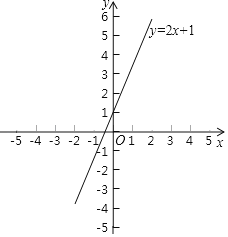
(1)求这个一次函数的关系式?
(2)画出函数图象.
(3)该函数图象与两个坐标轴围成的三角形的面积?
【答案】(1)y=2x﹣5;(2)如图所示,见解析;(3)该一次函数的图象与坐标轴围成的三角形的面积是![]() .
.
【解析】
(1)利用两直线的平行确定比例系数k,再将点(1,![]() )代入,即可确定解析式;
)代入,即可确定解析式;
(2)分别求出该直线与两坐标轴的交点坐标,再过这两个交点画直线即可;
(3)利用三角形的面积公式,即可求得面积.
解:(1)∵直线y=kx+b与直线y=2x+1平行,
∴k=2,
∵直线y=2x+b过点(1,﹣3),
∴2+b=﹣3,
∴b=﹣5,
∴一次函数的解析式为y=2x﹣5;
(2)∵y=2x﹣5,
∴当x=0时,y=﹣5;
当y=0时,x=2.5,
过(0,﹣5)、(![]() ,0)画直线,得到函数y=2x﹣5的图象,如图所示:
,0)画直线,得到函数y=2x﹣5的图象,如图所示:
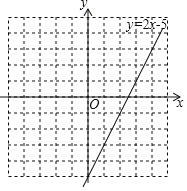
(3)如图,该一次函数的图象与坐标轴围成的三角形的面积是:![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题:
问题:“在平面内,已知分别有2个点,3个点,4个点,5个点,…,![]() 个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
探究:为了解决这个问题,希望小组的同学们,设计了如下表格进行探究:(为了方便研究问题,图中每条线段表示过线段两端点的一条直线)
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有个点时,直线条数为______;
(2)若某同学按照本题中的方法,共画了28条直线,求该平面内有多少个已知点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且点P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点P是线段MN关于点O的关联点.图1是点P为线段MN关于点O的关联点的示意图.

在平面直角坐标系xOy中,⊙O的半径为1.
(1)如图2,已知M(![]() ,
,![]() ),N(
),N(![]() ,﹣
,﹣![]() ),在A(1,0),B(1,1),C(
),在A(1,0),B(1,1),C(![]() ,0)三点中,是线段MN关于点O的关联点的是 ;
,0)三点中,是线段MN关于点O的关联点的是 ;
(2)如图3,M(0,1),N(![]() ,﹣
,﹣![]() ),点D是线段MN关于点O的关联点.
),点D是线段MN关于点O的关联点.
①∠MDN的大小为 ;
②在第一象限内有一点E(![]() m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
③点F在直线y=﹣![]() x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
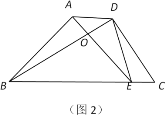
【题目】如图1,在四边形ABCD中,∠BAD=∠BDC=90°,AB=AD,∠DCB=60°,CD=8.
(1)若P是BD上一点,且PA=CD,求∠PAB的度数.
(2)①将图1中的△ABD绕点B顺时针旋转30°,点D落在边BC上的E处,AE交BD于点O,连接DE,如图2,求证:DE2=DODB;
②将图1中△ABD绕点B旋转α得到△A'BD'(A与A',D与D'是对应点),若CD'=CD,则cosα的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在四边形ABCD的边AB上任取一点
,在四边形ABCD的边AB上任取一点![]() 点P不与A,B重合
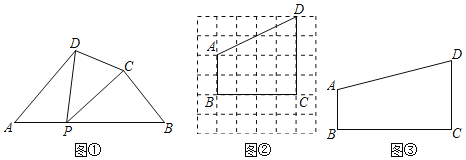
点P不与A,B重合![]() ,分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点“.
,分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点“.
解决问题
![]() 如图
如图![]() ,
,![]() ,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.
,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.
![]() 如图
如图![]() ,在四边形ABCD中,A,B,C,D四点均在正方形网格
,在四边形ABCD中,A,B,C,D四点均在正方形网格![]() 网格中每个小正方形的边长为
网格中每个小正方形的边长为![]() 的格点
的格点![]() 即每个小正方形的顶点
即每个小正方形的顶点![]() 上,试在图
上,试在图![]() 中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;
中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;
![]() 如图
如图![]() ,在四边形ABCD中,
,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() 点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.
点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
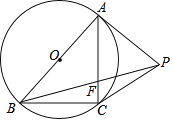
【题目】如图,PA与⊙O相切于点A,AB是⊙O的直径,在⊙O上存在一点C满足PA=PC,连结PB、AC相交于点F,且∠APB=3∠BPC,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地农产品专卖店收购了一种非常受欢迎的土特产,该店以![]() 元/千克收购了这种土特产
元/千克收购了这种土特产![]() 千克,若立即销往外地,每千克可以获利
千克,若立即销往外地,每千克可以获利![]() 元.根据市场调查发现,该种土特产的销售单价每天上涨
元.根据市场调查发现,该种土特产的销售单价每天上涨![]() 元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过
元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过![]() 天,在贮藏过程中平均每天损耗
天,在贮藏过程中平均每天损耗![]() 千克.
千克.
(1)若商家将这批土特产贮藏![]() 天后一次性出售,请完成下列表格:
天后一次性出售,请完成下列表格:
每千克土特产售价(单位:元) | 可供出售的土特产质量(单位:克) | |
现在出售 |
|
|
|
|
|
(2)将这批土特产贮藏多少天后一次性出售最终可获得总利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com