
 解:(1)①根据折叠的性质可得△ABE与△PBE关于直线BE对称,则正确;
解:(1)①根据折叠的性质可得△ABE与△PBE关于直线BE对称,则正确;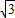 ,
,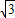 ,
, )2+12,
)2+12,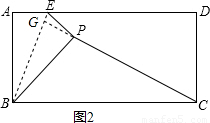
 =
=
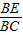 =
=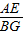 ,
,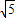 ,BG=
,BG=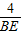 =
=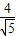 ,
, =PE•PB×
=PE•PB×
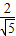 ,CG2=42-(
,CG2=42-( )2
)2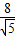
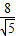 -
-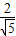 =
=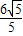 ≈2.7.
≈2.7.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
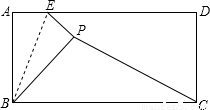
 (2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.
(2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
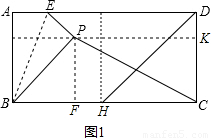
 如图,有一张矩形纸片ABCD,AB=4,AD=3,P为AB中点,点E在AD上,将△PBC,△PAE翻折分别得到△PCF和△PEG,折痕分别为PC、PE,且点F在PG上,则AE长为
如图,有一张矩形纸片ABCD,AB=4,AD=3,P为AB中点,点E在AD上,将△PBC,△PAE翻折分别得到△PCF和△PEG,折痕分别为PC、PE,且点F在PG上,则AE长为| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com