
【题目】汽车驾驶员坐在驾驶座位上,其视线观察不到的地方叫“汽车盲区”.如图是一辆汽车的“车头盲区”示意图,其中AC⊥BC,DE⊥BC,驾驶员所处位置的高度AC为1.4米,驾驶员座位AC与车头DE之间距离为2米,当驾驶员从A点观察车头D点时,其视线的俯角为12°,点A、D、B在同一直线上.
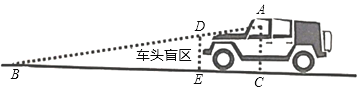
(1)请直接写出∠ABC的度数;
(2)求“车头盲区”点B、E之间的距离.(结果精确到0.1米)参考数据:sin12°=0.20,cas12°=0.99,tan12°=0.21
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】有甲、乙、丙三个不透明的布袋,甲袋中装有2个相同的小球,它们分别标有字母A和B;乙袋中装有3个相同的小球,它们分别标有字母C、D和E;丙袋中装有2个相同的小球,它们分别标有字母H和I.从三个布袋中各随机取出一个小球.求:(1)取出的3个小球恰好有2个元音字母的概率;(2)取出的3个小球全是辅音字母的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.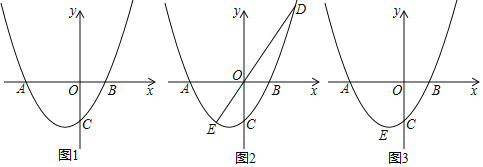
(1)如图1,分别求![]() 的值;
的值;
(2)如图2,点![]() 为第一象限的抛物线上一点,连接
为第一象限的抛物线上一点,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 为第一象限的抛物线上一点,过点
为第一象限的抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 为第二象限的抛物线上一点,且点
为第二象限的抛物线上一点,且点![]() 与点
与点![]() 关于抛物线的对称轴对称,连接
关于抛物线的对称轴对称,连接![]() ,设
,设![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为第三象限的抛物线上一点,分别连接
为第三象限的抛物线上一点,分别连接![]() ,满足
,满足![]() ,
,![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被哦感染.
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
(3)![]() 轮(
轮(![]() 为正整数)感染后,被感染的电脑有________台.
为正整数)感染后,被感染的电脑有________台.
查看答案和解析>>
科目:初中数学 来源: 题型:
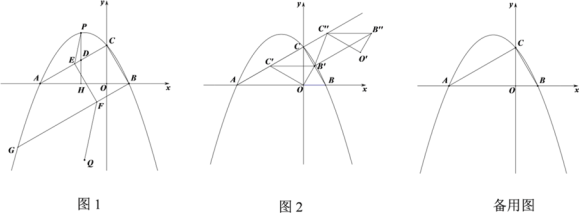
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
(1)如图1,求直线BC的解析式;
(2)如图1,线段AC上方抛物线上有一动点P,PD⊥x轴于点H,交线段AC于点D,直线BG∥AC,交抛物线于点G,点F是直线BC上一动点,FE∥BC交AC于点E,点Q是点A关于直线BG的对称点,连接PE、QF.当线段PD取最大值时,求PE+EF+QF的最小值及点E的坐标;
(3)如图2,将△BOC绕点O逆时针旋转至△B′O C′的位置,点B、C的对应点分别为点B′、C′,点B′恰好落在BC上.将△B′O C′沿直线AC平移,得到△B′′O ′ C′′,点B′、C′、O的对应点分别为点B′′、C′′、O ′,连接B ′ B′′、B ′C′′,△B ′B′′C′′是否能为等腰三角形?若能,请直接写出所有符合条件的C′′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,E为边BC上的一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMNP和点同时停止运动.设运动时间为t秒,解答问题:

(1)在整个运动过程中,当点G在线段AE上时,求t的值;
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形,若存在,求出t的值;若不存在,说明理由;
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t的函数关系式以及自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
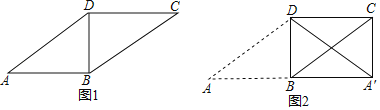
【题目】如图1,在平行四边形ABCD中,对角线BD⊥AB,以BD为对称轴将△ABD翻折,点A的对应点为A′,连接A′C,得到图2.
推理证明
(1)求证:四边形A′BDC是矩形;
实践操作
(2)在图1中将△ABD或△BDC进行平移、旋转或轴对称变换,重新构造一个特殊四边形.
要求:①画出图形,标明字母;②写出构图过程及构造的特殊四边形的名称.(不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com