
【题目】在等腰△ABC中,
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将 线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
…
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的数量关系,这个数量关系是 . (直接给出结论无须证明)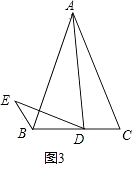
【答案】
(1)30°
(2)
① 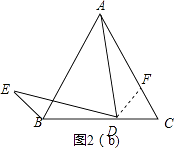
②思路1:如图2(a),连接AE,
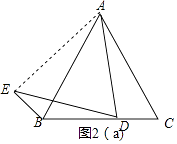
∵AD=DE,∠ADE=60°,
∴△ADE是等边三角形,
∵△ABC是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAD=60°,
∴∠EAB=∠CAD,
在△AEB△与ADC中, 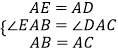 ,
,
∴△AEB≌△ADC,
∴CD=BE;
思路2:过点D作DF∥AB,交AC于F,
∵△ABC是等边三角形,
∴AC=BC,∠BAC=60°,
∵DF∥AB,
∴∠DFC=60°,
∴△CDF是等边三角形,
∴∠ADE=∠ACB=∠ABC=60°,
∴∠DAF=∠EDB,
在△ADF与△DEB中, 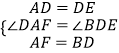 ,
,
∴△ADF≌△DEB,
∴DF=BE=CD;
思路3:如图2(c),延长CB至G,使BG=CD,∵△ABC是等边三角形,
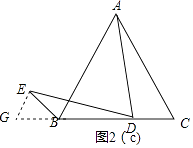
∴AC=BC,∠BAC=60°,
∵CD=BG,
∴DG=AC,∴∠ADE=∠ACB=∠ABC=60°,
∴∠DAF=∠EDB,
在△ADC与△DEG中, 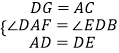 ,
,
∴△ADC≌△DEG,
∴CD=EG=BG=60°,
∴BE=BG=CD;
(3)k(BE+BD)=AC
【解析】解:(1.)∵△ABC是等边三角形,D为线段BC中点,
∴∠BAD=∠CAD= ![]() ∠BAC=30°,
∠BAC=30°,
∵线段AD关于直线AB的对称线段为线段AE,
∴AB⊥DE,
∴∠BDE=30°;
故答案为:30°;
(3.)k(BE+BD)=AC,
如图3,连接AE,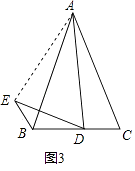
∵AC=kBC,AD=kDE,且∠ADE=∠C,
∴△ADE∽△ACB,
∴∠AED=∠ABC,∠EAD=∠BAC,
∴∠EAB=∠DAC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠AED=∠ADE,
∴AE=AD,
在△AEB△与ADC中, 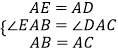 ,
,
∴△AEB≌△ADC,
∴CD=BE;
∵BC=BD+CD,
∴BC=BD+BE,
∵AC=kBC,
∴AC=k(BD+BE),
故答案为:k(BE+BD)=AC.
(1)根据等边三角形的性质得到∠BAD=∠CAD= ![]() ∠BAC=30°,由线段AD关于直线AB的对称线段为线段AE,得到AB⊥DE,于是得到结论;
∠BAC=30°,由线段AD关于直线AB的对称线段为线段AE,得到AB⊥DE,于是得到结论;
(2.)思路1:如图2(a),连接AE,思路2:过点D作DF∥AB,交AC于F,思路3:如图2(c),延长CB至G,使BG=CD,根据全等三角形的判定和性质即可得到结论;
(3.)如图3,连接AE,根据已知条件得到△ADE∽△ACB,根据相似三角形的性质得到∠AED=∠ABC,∠EAD=∠BAC,于是得到∠EAB=∠DAC,根据全等三角形的性质得到CD=BE;根据线段的和差即可得到结论.


科目:初中数学 来源: 题型:
【题目】甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
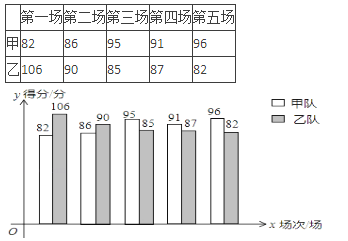
(1)分别计算甲乙两队5场比赛成绩的平均分.
(2)就这5场比赛,分别计算两队成绩的极差;
(3)就这5场比赛,分别计算两队成绩的方差;
(4)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、极差、方差以及获胜场数这四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
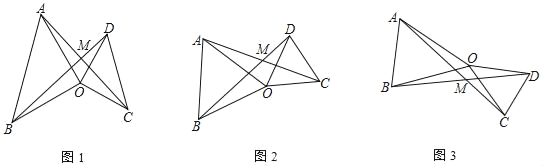
(1)如图1,当α=90°时,∠AMD的度数为 °
(2)如图2,当α=60°时,∠AMD的度数为 °
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
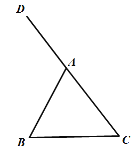
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 的一个外角,根据要求进行尺规作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
的一个外角,根据要求进行尺规作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
(1)作![]() 的平分线
的平分线![]() .
.
(2)作线段![]() 的垂直平分线,与
的垂直平分线,与![]() 交于点
交于点![]() ,与
,与![]() 边交于点
边交于点![]() ,判断线段
,判断线段![]() 是否也被
是否也被![]() 垂直平分,并说明理由.
垂直平分,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一点![]() 从数轴上表示
从数轴上表示![]() 的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
(1)写出第一次移动后这个点在数轴上表示的数;
(2)写出第![]() 次移动后这个点在数轴上表示的数;
次移动后这个点在数轴上表示的数;
(3)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象如图,则下列说法:①
的图象如图,则下列说法:①![]() ;②
;② ![]() 是方程
是方程![]() 的解;③若点
的解;③若点![]() ,
,![]() 是这个函数的图象上的两点,且
是这个函数的图象上的两点,且![]() ,则
,则![]() ;④当
;④当![]() ,函数的值
,函数的值![]() ,则
,则![]() .其中正确的个数为( )
.其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com