
【题目】某校开展“走进中国数学史”为主题的知识竞赛活动,八、九年级各有200名学生参加竞赛,为了解这两个年级参加竞赛学生的成绩情况,从中各随机抽取20名学生的成绩,数据如下:
八年级 | 91 | 89 | 77 | 86 | 71 | 九年级 | 84 | 93 | 66 | 69 | 76 |
51 | 97 | 93 | 72 | 91 | 87 | 77 | 82 | 85 | 88 | ||
81 | 92 | 85 | 85 | 95 | 90 | 88 | 67 | 88 | 91 | ||
88 | 88 | 90 | 64 | 91 | 96 | 68 | 97 | 99 | 88 |
整理上面数据,得到如下统计表:
成绩 人数 年级 |
|
|
|
|
|
八年级 | 1 | 1 | 3 | 7 | 8 |
九年级 | 0 | 4 | 2 | 8 | 6 |
样本数据的平均数、中位数、众数、方差如下表所示:
统计表 年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 83.85 | 88 | 91 | 127.03 |
九年级 | 83.95 | 87.5 | | 99.45 |
根据以上信息,回答下列问题:
(1)写出上表中众数![]() 的值.
的值.
(2)试估计八、九年级这次选拔成绩80分以上的人数和.
(3)你认为哪个年级学生的竞赛成绩较好?说明你的理由.(至少从两个不同的角度说明推断的合理性)
【答案】(1)88;(2)290人;(3)理由见解析.
【解析】
(1)根据众数的定义直接解答即可;
(2)先求出在随机抽取20名学生的成绩中80分以上的人数所占的百分比,再乘以总人数,即可得出答案;
(3)根据给出的平均数和方差分别进行分析,即可得出答案.
(1)∵88出现了4次,出现的次数最多,
∴众数m的值为88.
(2)![]()
![]()
![]() (人)
(人)
所以估计八、九年级这次选拔成绩80分以上的人数和约为290人.
(3)我认为九年级学生的竞赛成绩比较好,理由如下:
①九年级学生竞赛成绩的平均数较高,表示九年级竞赛成绩较好;
②九年级学生竞赛成绩的方差小,表示九年级学生竞赛成绩比较集中,整体水平较好.
另解:
我认为八年级学生竞赛成绩比较好,理由如下:
①中位数较高,表示八年级竞赛成绩较好;
②八年级学生竞赛成绩的众数较高,表示八年级学生多数成绩较好.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
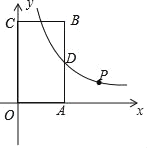
【题目】如图,矩形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,点B的坐标为(4,m)(5≤m≤7),反比例函数y=![]() (x>0)的图象交边AB于点D.
(x>0)的图象交边AB于点D.
(1)用m的代数式表示BD的长;
(2)设点P在该函数图象上,且它的横坐标为m,连结PB,PD
①记矩形OABC面积与△PBD面积之差为S,求当m为何值时,S取到最大值;
②将点D绕点P逆时针旋转90°得到点E,当点E恰好落在x轴上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
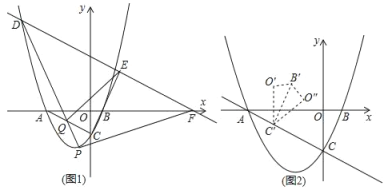
【题目】在平面直角坐标系中,抛物线y=![]() 交x轴于点A、B(点A在点B的左侧),交y轴于点C.
交x轴于点A、B(点A在点B的左侧),交y轴于点C.
(1)如图,点D是抛物线在第二象限内的一点,且满足|xD﹣xA|=2![]() ,过点D作AC的平行线,分别与x轴、射线CB交于点F、E,点P为直线AC下方抛物线上的一动点,连接PD交线段AC于点Q,当四边形PQEF的面积最大时,在y轴上找一点M,x轴上找一点N,使得PM+MN﹣
,过点D作AC的平行线,分别与x轴、射线CB交于点F、E,点P为直线AC下方抛物线上的一动点,连接PD交线段AC于点Q,当四边形PQEF的面积最大时,在y轴上找一点M,x轴上找一点N,使得PM+MN﹣![]() NB取得最小值,求这个最小值;
NB取得最小值,求这个最小值;
(2)如图2,将△BOC沿着直线AC平移得到△B′O′C′,再将△B'O′C′沿B′C′翻折得到△B′O″C′,连接BC′、O″B,则△C′BO″能否构成等腰三角形?若能,请直接写出所有符合条件的点O″的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度,某校随机抽查部分学生,对他们最喜欢的体育项目(每人只选一项)进行了问卷调查,并将统计数据绘制成如下两幅不完整的统计图:
请解答下列问题:
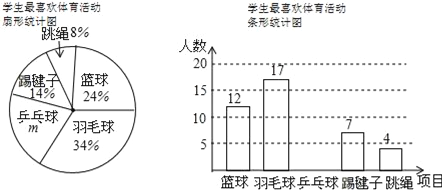
(1)m= %,这次共抽取了 名学生进行调查;请补全条形统计图;
(2)若全校有800名学生,则该校约有多少名学生喜爱打篮球?
(3)学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
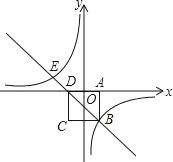
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数![]() 的图象交于点B、E.
的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】y=ax2+bx+c的图象如图所示,则下列4个代数式a+2b+c,2a+b+c,3a+2b+c,-![]() ,其中值一定大于1的个数是( )
,其中值一定大于1的个数是( )
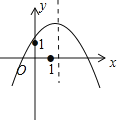
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰直角![]() 中,
中,![]() ,
,![]() 过点
过点![]() ,
,![]() 的圆交
的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() .
.
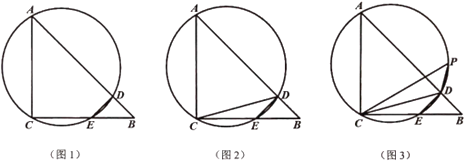
(1)若![]() ,
,![]() ,分别求
,分别求![]() ,
,![]() 的长
的长
(2)如图2,连结![]() ,若
,若![]() ,
,![]() 的面积为10,求
的面积为10,求![]() .
.
(3)如图3,在圆上取点![]() 使得
使得![]() (点
(点![]() 与点
与点![]() 不重合),连结
不重合),连结![]() ,且点
,且点![]() 是
是![]() 的内心
的内心
①请你画出![]() ,说明画图过程并求
,说明画图过程并求![]() 的度数.
的度数.
②设![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的内切圆半径长.
的内切圆半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
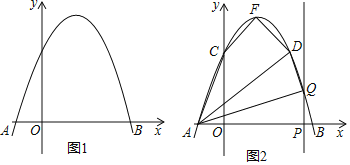
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com