
【题目】已知![]() 为
为![]() 直径,
直径,![]() 是直径
是直径![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() ,
,![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 上一点(不与点
上一点(不与点![]() ,
,![]() 重合),且
重合),且![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() .
.
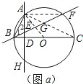
![]() 如图
如图![]() ,当点
,当点![]() 在线段
在线段![]() 上时,试判断
上时,试判断![]() 与
与![]() 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
![]() 当点
当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,其它条件不变.
时,其它条件不变.

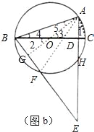
①请你在图![]() 中画出符合要求的图形,并参照图
中画出符合要求的图形,并参照图![]() 标记字母;
标记字母;
②判断![]() 中的结论是否还成立,请说明理由.
中的结论是否还成立,请说明理由.
【答案】见解析
【解析】
(1)AE=BE,可根据垂径定理得出弧AB=弧BH,已知了弧AB=弧AF,因此弧BH=弧AF,根据圆周角定理可得出∠BAH=∠ABF根据等角对等边即可得出AE=BE.(方法不唯一)
(2)结论不变,证法同(1),根据垂径定理可得出弧AC=弧CH,因此弧AB=弧BH,由于弧AB=弧AF,因此弧AF=弧BH,即∠BAE=∠ABE,因此AE=BE.
![]()
证法①:
∵![]() 为
为![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.
证法②:
连![]() ,
,![]()
∵![]() 是
是![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
∴![]() ,
,![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.
证法③:
连接![]() ,交
,交![]() 于点
于点![]()
∵![]()
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()

![]() ①所画图形如图所示,
①所画图形如图所示,![]() 成立
成立
证法①:
∵![]() 是
是![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
又![]()
∴![]()
∴![]()
∴![]() .
.
证法②:
连接![]() ,
,![]()
∵![]() 是
是![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]() .
.
证法③:
连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]()
∵![]() ,
,![]() 过圆心
过圆心
∴![]()
又∵![]() 于点
于点![]()
∴![]()
又∵![]() 为
为![]() 直径,
直径,![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点O是边AB、AC垂直平分线的交点,点E是∠ABC、∠ACB角平分线的交点,若∠O+∠E=180°,则∠A=_____度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上.当△PMN周长最小时,下列结论:①∠MPN等于120°;②∠MPN等于100°;③△PMN周长最小值为4;④△PMN周长最小值为8,其中正确的是( )

A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(0,3)、B(3,0)、C(﹣3,0).

(1)过B作直线MN⊥AB,P为线段OC上的一动点,AP⊥PH交直线M于点H,证明:PA=PH.
(2)在(1)的条件下,若在点A处有一个等腰Rt△APQ绕点A旋转,且AP=PQ,∠APQ=90°,连接BQ,点G为BQ的中点,试猜想线段OG与线段PG的数量关系与位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,E在线段AC上,连接AD, BE的延长线交AD于F.
(1)猜想线段BE、AD的数量关系和位置关系:_______________(不必证明);
(2)当点E为△ABC内部一点时,使点D和点E分别在AC的两侧,其它条件不变.
①请你在图2中补全图形;
②(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.
如:![]() ,
,![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,
,![]() 这三个数都是神秘数.
这三个数都是神秘数.
(1)![]() 是神秘数吗?为什么?
是神秘数吗?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 取非负整数),由这两个连续偶数构造的神秘数是
取非负整数),由这两个连续偶数构造的神秘数是![]() 的倍数吗?为什么?
的倍数吗?为什么?
(3)①若长方形相邻两边长为两个连续偶数,试说明其周长一定为神秘数.
②在①的条件下,面积是否为神秘数?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com