
����Ŀ����ͼ����Rt��ABC�У���A��90����AC��3��AB��4������P�ӵ�A��������AB������ÿ��2����λ���ȵ��ٶ����յ�B�˶�����QΪ�߶�AP���е㣬����P������PM��AB����PM��3AQ����PQ��PMΪ��������PQNM�����P���˶�ʱ��Ϊt�룮
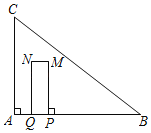
��1���߶�MP�ij�Ϊ�� �����ú�t�Ĵ���ʽ��ʾ����
��2�����߶�MN���BC�й�����ʱ����t��ȡֵ��Χ��
��3������N����ABC�ڲ�ʱ�������PQNM����ABC�ص�����ͼ�ε����ΪS����S��t֮��ĺ�����ϵʽ��
��4������M����ABC������������ֱ�߾������ʱ��ֱ��д����ʱt��ֵ��
���𰸡���1��3t����2������������t��ֵΪ![]() ��t��
��t��![]() ����3��S��
����3��S�� ����4������������t��ֵΪ
����4������������t��ֵΪ![]() ��
��![]() ��
��![]() .
.
��������
��1������·�̡��ٶȡ�ʱ��Ĺ�ϵ�ٽ��������.
��2���ֱ����M��N����BC��ʱ��t�ķ�Χ���ɣ�
��3�����ص������Ǿ���PQNM�������PQNEF����������н�ɣ�
��4���������������Σ�����M���ڡ�ABC�Ľ�ƽ����BF��ʱ����������.��FELBC��E������M���ڡ�ACB�Ľ�ƽ������ʱ������������EFLBC��F������M���ڡ�ABC�ġ�ACB����ǵ�ƽ������ʱ����������.�ֱ���⼴�ɽ��.
�⣺��1��������AP��2t��AQ��PQ��t��
��PM��3PQ��
��PM��3t��
�ʴ�Ϊ3t��
��2����ͼ2��1�У�����M����BC��ʱ��

��PM��AC��
��![]() ��
��
��![]() ��
��
���t��![]()
��ͼ2��2�У�����N����BC��ʱ��

��NQ��AC��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
��������������������t��ֵΪ![]() ��t��
��t��![]() ��
��
��3����ͼ3��1�У���0��t��![]() ʱ���ص������Ǿ���PQNM��S��3t2
ʱ���ص������Ǿ���PQNM��S��3t2

��ͼ3��2�У���![]() ��t��
��t��![]() ʱ���ص������������PQNEF��
ʱ���ص������������PQNEF��

S��S����PQNM��S��EFM��3t2��![]() [3t��
[3t��![]() ��4��2t��]
��4��2t��]![]() [3t��
[3t��![]() ��4��2t��]����
��4��2t��]����![]() t2+18t��6��
t2+18t��6��
���������� ��
��
��4����ͼ4��1�У�����M���ڡ�ABC�Ľ�ƽ����BF��ʱ��������������FE��BC��E��
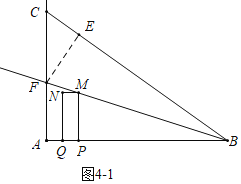
�ߡ�FAB����FEB��90�㣬��FBA����FBE��BF��BF��
���BFA�ա�BFE��AAS����
��AF��EF��AB��BE��4����AF��EF��x��
�ߡ�A��90�㣬AC��3��AB��4��
��BC��![]() ��5��
��5��
��EC��BC��BE��5��4��1��
��Rt��EFC������x2+12����3��x��2��
���x��![]() ��
��
��PM��AF��
��![]() ��
��
��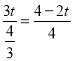 ��
��
��t��![]()
��ͼ4��2�У�����M���ڡ�ACB�Ľ�ƽ������ʱ������������EF��BC��F��
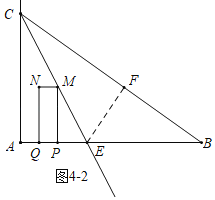
ͬ����֤����ECA�ա�ECF��AAS����
��AE��EF��AC��CF��3����AE��EF��y��
��BF��5��3��2��
��Rt��EFB������x2+22����4��x
���x��![]() ��
��
��PM��AC��
��![]() ��
��
�� ��
��
���t��![]() ��
��
��ͼ4��3�У�����M���ڡ�ABC�ġ�ACB����ǵ�ƽ������ʱ������������

��MC���ӳ��߽�BA���ӳ�����E����EF��BC��BC���ӳ����ڷ֣�
ͬ����֤��AC��CF��3��EF��AE����EF��EA��x��
��Rt��EFB������x2+82����x+4��2��
���x��6��
��AC��PM��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
��������������������t��ֵΪ![]() ��
��![]() ��
��![]() .
.


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
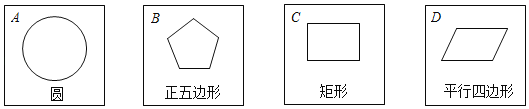
����Ŀ�������ŷ�����ȫ��ͬ��ֽ��![]() ��������ֱ����ĸ���ͬ�ļ���ͼ�Σ�������ֽ��ϴ�����泯��������������ϣ�
��������ֱ����ĸ���ͬ�ļ���ͼ�Σ�������ֽ��ϴ�����泯��������������ϣ�
��1��������ֽ�����������һ�ţ�����������ͼ�������ĶԳ�ͼ�εĸ������� ����
��2��С����С��Լ����һ����Ϸ�������Ϊ������С���������һ�ţ����Żأ�����С����ʣ�µ�ֽ�����������һ�ţ�����������������ͼ�μ�����Գ�ͼ���������ĶԳ�ͼ�Σ���С����ʤ������С����ʤ�������Ϸ��ƽ�������б���������״ͼ��˵�����ɣ���ֽ����![]() ��ʾ��������ƽ�������æ��һ����Ϸ����ʹ��Ϸ��ƽ��
��ʾ��������ƽ�������æ��һ����Ϸ����ʹ��Ϸ��ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� 24 �춬�»Ὣ�� 2022 ���ڱ������żҿھ��У����»����Ŀ�л�ѩ������̨��ѩ����ɽ��ѩ�����廬ѩ�ȣ�����������̵��ٻ����ٶȻ��������������ȣ����������ȣ���ͼ���� 5 ����״����С���ʵؾ���ͬ�Ŀ�Ƭ������ֱ�ӡ�и�ɽ��ѩ���ٶȻ����������廬ѩ���������ֲ�ͬ��ͼ����������ȫ��ͬ���ֽ��� 5 �ſ�Ƭϴ�Ⱥ��������·��������ϣ����������ȡһ�ţ�����Ŀ�Ƭ����ǡ���ǻ�ѩ��Ŀͼ���ĸ����ǣ� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����мס��ҡ���������ɵ�����ѵ��С�飬��������֮����л��ഫ����ϰ�������һ�������������������һ�������м�������һ�Σ��������������Σ�
��1������ʼʱ�����ڼ����У�����һ�δ�����������ڱ������еĸ������� ��
��2������ʼʱ�����ڼ����У����������δ���������ҵ����еĸ��ʣ������û���״ͼ���б��ȷ�����⣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¸�ͼ�����ɱ߳�Ϊ1��С��������ɵ�����ͼ�еĵ�A��B��C��D���ڸ���ϣ�

��1����ͼ���У�PC��PB���� ��
��2������������̶ȵ�ֱ����ͼ�������ۼ�����д������
����ͼ�ڣ���AB����һ��P��ʹAP��3��
����ͼ�ۣ���BD����һ��P��ʹ��APB�ס�CPD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬʱ����3öӲ������Ϸ������1ԪӲ��1ö��5��Ӳ����ö��
��1����3öӲ��ͬʱ���泯�ϵĸ��ʣ�
��2��С�š�С��Լ�������泯�ϰ���ֵ�㣬���泯�ϰ�0Ԫ�㣮3ö��غ�����ֵ��Ϊ1.5Ԫ����С�Ż��1�֣�����ֵ��Ϊ1Ԫ����С����1�֣�˭�ȵõ�10�֣�˭��ʤ�����������Ϸ�Ƿ�ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����n��һ����λ����������n�ĸ�λ���ִ���ʮλ���֣����nΪ����λ������������13��35��56�ȣ�����ij����ѧȤζ��У�ÿλ�μ������������1��2��3��4��5��6���ɵ����еġ���λ���������������ȡ1��������ֻ�ܳ�ȡһ�Σ�
��1��д�����и�λ������5�ġ���λ����������
��2�������б�������״ͼ�����ȡ�ġ���λ���������ĸ�λ������ʮλ����֮���ܱ�10�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ��3��b+d+f��0������k��
��3��b+d+f��0������k��![]() ��
��
��1����k��ֵ��
��2����x1��x2�Ƿ���x2��3x+k��2��0����������x12+x22��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���ACB��90����AB��14![]() ����D��E�ֱ��ڱ�AB��BC�ϣ����߶�ED�Ƶ�E����ʱ�뷽����ת90���õ�EF��
����D��E�ֱ��ڱ�AB��BC�ϣ����߶�ED�Ƶ�E����ʱ�뷽����ת90���õ�EF��

��1����ͼ1����AD��BD����E���C�غϣ�AF��DC�ཻ�ڵ�O����ֱ��д��BD��DO��������ϵ��
��2����֪��GΪAF���е㣮
����ͼ2����AD��BD��CE��2����DG�ij���
����ͼ3����DG��BC��EC��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com