
【题目】如图①,(1)已知∠ABC,射线ED∥AB,过点E作∠DEF=∠ABC,试说明BC∥EF;
(2)如图②,已知∠ABC,射线ED∥AB,∠ABC+∠DEF=180°.判断直线BC与直线EF的位置关系,并说明理由;
(3)根据以上探究,你发现了一个什么结论?请你写出来;
(4)如图③,已知AC⊥BC,CD⊥AB,DE⊥AC,HF⊥AB,若∠1=48°,试求∠2的度数.



【答案】(1)(2)(3)见解析;(4)132°.
【解析】试题分析:(1)根据平行线的判定和性质即可得到结论;
(2)根据平行线的判定和性质即可得到结论;
(3)由(1)、(2)的结论即可得到结果;
(4)根据平行线的判定和性质即可得到结论.
试题解析:
(1)∵ED∥AB,
∴∠B=∠DOC,
∵∠DEF=∠ABC,
∴∠DOC=∠DEF,
∴BC∥EF;
(2)∵ED∥AB,
∴∠B=∠BOE,
∵∠ABC+∠DEF=180°,
∴∠BOE+∠DEF=180°,
∴BC∥EF;
(3)由(1)、(2)可得,如果两个角相等或互补且一边平行,则另一边也平行;
(4)∵AC⊥BC,DE⊥AC,
∴DE∥BC,
∴∠DCB=∠1=48°,
∵CD⊥AB,HF⊥AB,
∴CD∥HF,
∴∠2=180°-∠DCB=132°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2![]() ,求阴影部分的面积.
,求阴影部分的面积.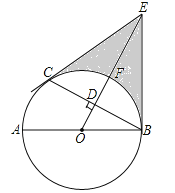
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.
(1)若∠ABC=70°,∠ACB=50°,则∠BPC= °;
(2)求证:∠BPC=180°﹣![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接河北省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
,A绳子,B绳子,C绳子长度(米),8,6,4单价(元/条),12,8,6
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为____________,其解为x1=-4,x2=-5;
(2)根据这类方程特征,写出第n个方程为________________,其解为x1=-n,x2=-n-1;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
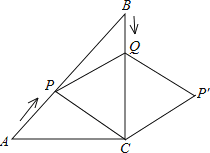
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A.![]() B.2 C.2
B.2 C.2![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.

(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系[式;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探索:
在图①~③中,△ABC的面积为a.

(1)如图①,延长△ABC的边BC到点D,使CD=BC,连接DA,若△ACD的面积为S1,则S1=________(用含a的式子表示);
(2)如图②,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若△DEC的面积为S2,则S2=________(用含a的式子表示),请说明理由;
(3)如图③,在图②的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF,若阴影部分的面积为S3,则S3=________(用含a的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com