
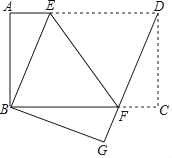
【题目】在矩形纸片ABCD中,AB=6,BC=8,现将纸片折叠,使点D与点B重合,折痕为EF,连接DF.
(1)说明△BEF是等腰三角形;
(2)求折痕EF的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据折叠得出∠DEF=∠BEF,根据矩形的性质得出AD∥BC,求出∠DEF=∠BFE,求出∠BEF=∠BFE即可;
(2)过E作EM⊥BC于M,则四边形ABME是矩形,根据矩形的性质得出EM=AB=6,AE=BM,根据折叠得出DE=BE,根据勾股定理求出DE、在Rt△EMF中,由勾股定理求出即可.
(1)∵现将纸片折叠,使点D与点B重合,折痕为EF,∴∠DEF=∠BEF.
∵四边形ABCD是矩形,∴AD∥BC,∴∠DEF=∠BFE,∴∠BEF=∠BFE,∴BE=BF,即△BEF是等腰三角形;
(2)过E作EM⊥BC于M,则四边形ABME是矩形,所以EM=AB=6,AE=BM.
∵现将纸片折叠,使点D与点B重合,折痕为EF,∴DE=BE,DO=BO,BD⊥EF.
∵四边形ABCD是矩形,BC=8,∴AD=BC=8,∠BAD=90°.
在Rt△ABE中,AE2+AB2=BE2,即(8﹣BE)2+62=BE2,解得:BE=![]() =DE=BF,AE=8﹣DE=8﹣
=DE=BF,AE=8﹣DE=8﹣![]() =
=![]() =BM,∴FM=
=BM,∴FM=![]() ﹣
﹣![]() =
=![]() .
.
在Rt△EMF中,由勾股定理得:EF=![]() =
=![]() .
.
故答案为:![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
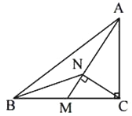
【题目】如图所示,在△ABC中,∠ACB=90°,AM是BC边的中线,CN⊥AM于N点,连接BN,求证:
(1)△MCN∽△MAC;
(2)∠NBM=∠BAM.
查看答案和解析>>
科目:初中数学 来源: 题型:
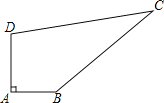
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 且点
且点![]() 在点
在点![]() 的右侧.点
的右侧.点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向以
方向以![]() /秒的速度运动,同时点
/秒的速度运动,同时点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向以
方向以![]() /秒的速度运动,在线段
/秒的速度运动,在线段![]() 上取点
上取点![]() ,使得
,使得![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒.当
秒.当![]() __________秒时,以
__________秒时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
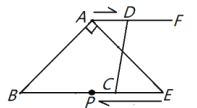
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() ,点
,点![]() 是射线
是射线![]() 上任意点(点
上任意点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() .
.

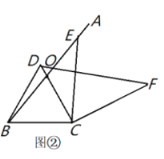
(1)如图①,猜想![]() 的度数是__________;
的度数是__________;
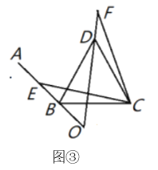
(2)如图②,图③,当![]() 是锐角或钝角时,其他条件不变,猜想
是锐角或钝角时,其他条件不变,猜想![]() 的度数,并选取其中一种情况进行证明;
的度数,并选取其中一种情况进行证明;
(3)如图③,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距20km.甲、乙两人都由A地去B地,甲骑自行车,平均速度为10km/h;乙乘汽车,平均速度为40km/h,且比甲晚1.5h出发.设甲的骑行时间为x(h)(0≤x≤2)
(1)根据题意,填写下表:
时间x(h) 与A地的距离 | 0.5 | 1.8 | _____ |
甲与A地的距离(km) | 5 |
| 20 |
乙与A地的距离(km) | 0 | 12 |
|
(2)设甲,乙两人与A地的距离为y1(km)和y2(km),写出y1,y2关于x的函数解析式;
(3)设甲,乙两人之间的距离为y,当y=12时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
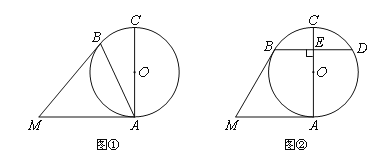
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com