
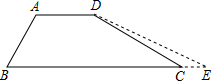
 为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12$\sqrt{3}$米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=$\frac{3}{13}$$\sqrt{3}$,则CE的长为8米.
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12$\sqrt{3}$米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=$\frac{3}{13}$$\sqrt{3}$,则CE的长为8米. 分析 分别过A、D作下底的垂线,设垂足为F、G.在Rt△ABF中,已知坡面长和坡角的度数,可求得铅直高度AF的值,也就得到了DG的长;在Rt△CDG中,由勾股定理求CG的长,在Rt△DEG中,根据正切函数定义得到GE的长;根据CE=GE-CG即可求解.
解答 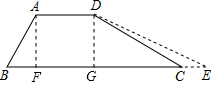 解:分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.
解:分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.
∵在Rt△ABF中,AB=12米,∠B=60°,
∴sin∠B=$\frac{AF}{AB}$,
∴AF=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,
∴DG=6$\sqrt{3}$.
∵在Rt△DGC中,CD=12$\sqrt{3}$,DG=6$\sqrt{3}$米,
∴GC=$\sqrt{C{D}^{2}-D{G}^{2}}$=18.
∵在Rt△DEG中,tanE=$\frac{3}{13}$$\sqrt{3}$,
∴$\frac{6\sqrt{3}}{GE}$=$\frac{3}{13}$$\sqrt{3}$,
∴GE=26,
∴CE=GE-CG=26-18=8.
即CE的长为8米.
故答案为8.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,锐角三角函数的定义,勾股定理.作辅助线构造直角三角形是解答此类题的一般思路.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
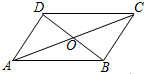 如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.
如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
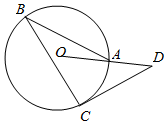 如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )| A. | 29° | B. | 32° | C. | 42° | D. | 58° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com