
 如图,抛物线y=ax2+bx-2经过点A(1,0)和点B(4,0),与y轴交于点C.
如图,抛物线y=ax2+bx-2经过点A(1,0)和点B(4,0),与y轴交于点C.分析 (1)根据A、B两点坐标待定系数法求解可得;
(2)作AD⊥BC,证△ABD∽△CBO得$\frac{AD}{CO}$=$\frac{AB}{BC}$,求出圆的半径AD的长即可得圆的面积;
(3)待定系数法求得直线BC解析式为y═$\frac{1}{2}$x-2,设平移后的直线解析式为y=$\frac{1}{2}$x+m,与抛物线的交点M(x1、$\frac{1}{2}$x1+m)、N(x2,$\frac{1}{2}$x2+m),由直线与抛物线相交得到关于x的方程及x1+x2=4,x1x2=2m+4,利用两点间的距离公式列出关于m的方程,解之可得答案.
解答 解:(1)将点A(1,0)、B(4,0)代入y=ax2+bx-2,
得:$\left\{\begin{array}{l}{a+b-2=0}\\{16a+4b-2=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2;
(2)当x=0时,y=-2,
∴点C(0,-2),即OC=2,
由A(1,0)、B(4,0)知OA=1、OB=4,
∴AB=3,BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
如图,过点A作AD⊥BC于点D,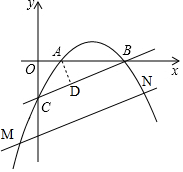
∴∠ADB=∠COB=90°,
∵∠ABD=∠CBO,
∴△ABD∽△CBO,
∴$\frac{AD}{CO}$=$\frac{AB}{BC}$,即$\frac{AD}{2}$=$\frac{3}{2\sqrt{5}}$,
解得AD=$\frac{3\sqrt{5}}{5}$,
∴以点A为圆心、AD长为半径作⊙A,此时⊙A与BC相切,
∴⊙A的面积为π•($\frac{3\sqrt{5}}{5}$)2=$\frac{9}{5}$π;
(3)设BC的解析式为y=kx+b,
将B(4,0)、C(0,-2)代入,得:$\left\{\begin{array}{l}{4k+b=0}\\{b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$,
∴直线BC的解析式为y=$\frac{1}{2}$x-2,
设平移后的直线解析式为y=$\frac{1}{2}$x+m,与抛物线的交点M(x1、$\frac{1}{2}$x1+m)、N(x2,$\frac{1}{2}$x2+m),
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+m}\\{y=-\frac{1}{2}{x}^{2}+\frac{5}{2}x-2}\end{array}\right.$得-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=$\frac{1}{2}$x+m,整理得x2-4x+2m+4=0,
∴x1+x2=4,x1x2=2m+4,
则MN=$\sqrt{({x}_{1}-{x}_{2})^{2}+(\frac{1}{2}{x}_{1}+m-\frac{1}{2}{x}_{2}-m)^{2}}$
=$\sqrt{({x}_{1}-{x}_{2})^{2}+\frac{1}{4}({x}_{1}-{x}_{2})^{2}}$
=$\sqrt{\frac{5}{4}({x}_{1}-{x}_{2})^{2}}$
=$\sqrt{\frac{5}{4}[({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}]}$
=$\sqrt{\frac{5}{4}({x}_{1}+{x}_{2})^{2}-\frac{5}{2}{x}_{1}{x}_{2}}$,
∵MN=2BC=4$\sqrt{5}$,
∴MN2=80,即$\frac{5}{4}$(x1+x2)2-$\frac{5}{2}$x1x2=80,
∴$\frac{5}{4}$×16-$\frac{5}{2}$×(2m+4)=80,
解得m=-14,
∴平移后直线MN的解析式为y=$\frac{1}{2}$x-14,
则平移的距离n=12.
点评 本题主要考查二次函数的综合问题,掌握待定系数法求函数解析式、相似三角形的判定和性质、两点间的距离公式等知识点是解题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{{(-2)}^{2}}$=-2 | ||
| C. | $\root{3}{-125}$=-5 | D. | -1的算术平方根是1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,有下列命题:①若∠1=∠2,则∠D=∠3;②若∠C=∠D,则∠3=∠C;③若∠A=∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则DF∥AC,其中正确的个数为( )
如图,有下列命题:①若∠1=∠2,则∠D=∠3;②若∠C=∠D,则∠3=∠C;③若∠A=∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则DF∥AC,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
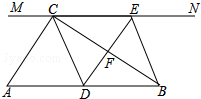 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
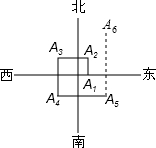 如图,一个机器人从O(0,0)点出发,向正东方向走3m,到达A1点,再向正北方向走6m到点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律走下去,当机器人走到点A7点时,A7点的坐标是( )
如图,一个机器人从O(0,0)点出发,向正东方向走3m,到达A1点,再向正北方向走6m到点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律走下去,当机器人走到点A7点时,A7点的坐标是( )| A. | (-12,12) | B. | (-9,12) | C. | (-12,-12) | D. | (-12,9) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com