
【题目】为了丰富学生的业余文化生活,某校教务处准备在大课间期间开设兴趣小组,预设科目为“舞蹈”“音乐”“电竞”“动漫”为了准确配备教室与师资,负责人制作了“你最喜欢的科目”的调查问卷,在校园随机调查后制作了两幅不完整的统计图,请你根据信息解答下面问题:
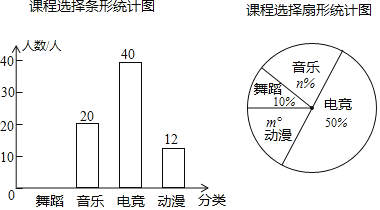
(1)本次调查中,参与问卷调查的人数为 ;
(2)扇形统计图中的m、n的值为 、 ,补全条形统计图;
(3)若该校有学生2000人,请你估计报名“电竞”的学生的人数为 ;
(4)最先报名“动漫”课程的三名学生中有两名男生一名女生,若随机抽取两名学生参与教室网线布设,求两名学生恰为一男一女的概率.
【答案】(1)80;(2)25,54,图详见解析;(3)1000;(4)![]() .
.
【解析】
(1)从两个统计图可得,“电竞”的有40人,占调查人数的50%,可求出调查人数;
(2)求出“音乐”20人所占的百分比,即可求出n的值,求出“动漫”12人所占的百分比,即可求出“动漫”所在的圆心角的度数,确定m的值;求出“舞蹈”的人数,即可补全条形统计图:
(3)样本估计总体,样本中“电竞”占50%,估计总体2000人的50%是报“电竞”的人数.
(4)用列表法列举出所有可能出现的结果,从中找出“一男一女”的结果数,即可求出相应的概率.
解:(1)40÷50%=80(人),
故答案为:80;
(2)20÷80=25%,m=360°×![]() =54°,
=54°,
80×10%=8(人),补全条形统计图如图所示:
故答案为:25,54;
(3)2000×50%=1000(人)
故答案为:1000;
(4)用列表法表示所有可能出现的结果如下:
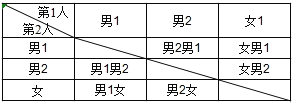
共有6种结果,其中一男一女的有4种,
∴两名学生恰为一男一女的概率为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 点的坐标为
点的坐标为![]() .
.


(1)求抛物线的函数表达式和![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)如图,设点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .记
.记![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴与![]() 交于点
交于点![]() (如图2),点
(如图2),点![]() 是抛物线上的一个动点,点
是抛物线上的一个动点,点![]() 是
是![]() 轴上的一个动点,当以
轴上的一个动点,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,求点
为顶点的四边形是平行四边形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外学习小组根据学习函数的经验,对函数y=x3﹣3x的图象与性质进行了探究.请补充完整以下探索过程:
(1)列表:
x | … | ﹣2 |
| ﹣1 |
| 0 |
| 1 |
| 2 | … |
y | … | ﹣2 | m | 2 |
| 0 |
| n |
| 2 | … |
请直接写出m,n的值;
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象;
(3)若函数y=x3﹣3x的图象上有三个点A(x1,y1),B(x2,y2),C(x3,y3),且x1<﹣2<x2<2<x3,则y1,y2,y3之间的大小关系为 (用“<”连接);
(4)若方程x3﹣3x=k有三个不同的实数根.请根据函数图象,直接写出k的取值范围.
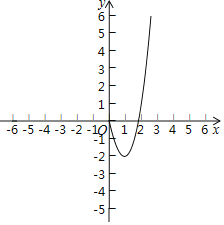
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高科技公司根据市场需求,计划生产A,B两种型号的医疗器械.其部分信息如下:
信息一:每台A型器械的售价为24万元,每台B型器械的售价为30万元,每台B型器械的生产成本比A型器械的生产成本多5万元.
信息二:若销售3台A型器械和5台B型器械,共获利37万元;
根据上述信息,解答下列问题:
(1)求每台A型器械、每台B型器械的生产成本各是多少万元?
(2)若A,B两种型号的医疗器械共生产80台,且该公司所筹生产医疗器械资金不少于1800万元,但不超过1810万元,且把所筹资金全部用于生产此两种医疗器械,根据市场调查,每台A型医疗器械的售价将会提高a万元(a>0),每台B型医疗器械的售价不会改变,该公司应该如何生产可以获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
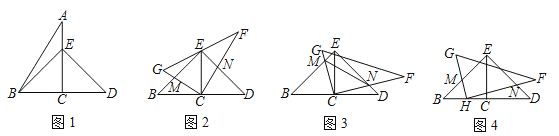
【题目】一副三角板如图1所置,其中AC边与等腰Rt△EBD斜边上的中线EC共线,以C点为旋转中心,顺时针转动△ACB,B、A两点分别于G、F两点对应,CG交BE边于点M,CF交DE边于N,已知旋转角为α,BC=2.
(问题发现)(1)如图2所示,若旋转角α(0°<α<30°)时,猜想CM与CN的数量关系,并写出你的推断过程;
(类比探究)(2)如图3所示,若旋转角α=75°时,(1)中的结论是否还成立? ,此时连接MN,请直接写出MN的长度为 ;
(拓展延伸)(3)在图3的基础上将△GCF向左平移至△GHF的位置,若DH=kBH,猜想线段HN与HM的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,点P在以C(-2,0)为圆心,1为半径的圆上,Q是AP的中点
(k>0)的图象交于A、B两点,点P在以C(-2,0)为圆心,1为半径的圆上,Q是AP的中点
(1)若AO=![]() ,求k的值;
,求k的值;
(2)若OQ长的最大值为![]() ,求k的值;
,求k的值;
(3)若过点C的二次函数y=ax2+bx+c同时满足以下两个条件:①a+b+c=0;②当a≤x≤a+1时,函数y的最大值为4a,求二次项系数a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是以BC为直径的半圆的中点,连接AB,点D是直径BC上一点,连接AD,分别过点B、点C向AD作垂线,垂足为E和F,其中,EF=2,CF=6,BE=8,则AB的长是( )
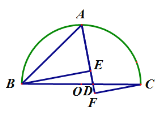
A.4B.6C.8D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com