
【题目】(本题满分8分)如图,南北方向线MN以西为我国领海,以东为公海.上午9时50分,我缉私艇A发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海驶来,便立即通知正在MN线上巡逻的缉私艇B.已知A,C两艇的距离是13海里,A,B两艇的距离是5海里,缉私艇B与C艇的距离是12海里,若C艇的速度不变,那么它最早会在什么时间进入我国领海?

科目:初中数学 来源: 题型:
【题目】如图,点A在数轴上表示的数是﹣2,点B表示+6,P、Q两点同时分别以1个单位/秒和3个单位/秒的速度从A、B两点出发,沿数轴规则运动
(1)求线段AB的长度;
(2)如果P、Q两点在数轴上相向移动,问几秒钟后PQ=![]() AB?
AB?
(3)如果P、Q两点在数轴上同时沿数轴负半轴方向移动(Q在P的左侧),若M、N分别是PA和BQ中点,问是否存在这样的时间t,使得线段MN=![]() AB?若存在,请求出t的值;若不存在,请说明理由.
AB?若存在,请求出t的值;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)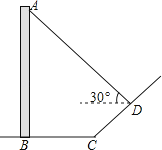
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.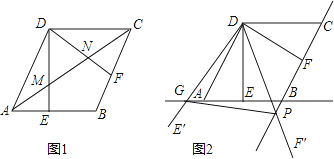
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN= ![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3 ![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图,在图1所给方格纸中,每个小正方形边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图2中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等.(分割线画成实线.)

(2)如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线L成轴对称的 ![]() ;
;
②请直线L上找到一点P,使得PC + PB的距离之和最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
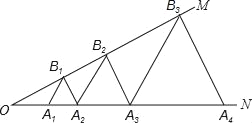
【题目】如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com