
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
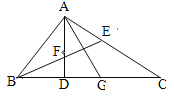
A. 1个 B. 2个 C. 3个 D. 4个
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,点A、B分别在直线OM、ON上,BC是∠ABN的平分线.
(1)如图1,若BC所在直线交∠OAB的平分线于点D时,尝试完成①、②两题:
①当∠ABO=30°时,∠ADB= °
②当点A、B分别在射线OM、ON上运动时(不与点O重合),试问:随着点A、B的运动,∠ADB的大小会变吗?如果不会,请求出∠ADB的度数;如果会,请求出∠ADB的度数的变化范围;
(2)如图2, 若BC所在直线交∠BAM的平分线于点C时,将△ABC沿EF折叠,使点C落在四边形ABEF内点C′的位置.求∠BEC′+∠AFC′ 的度数.
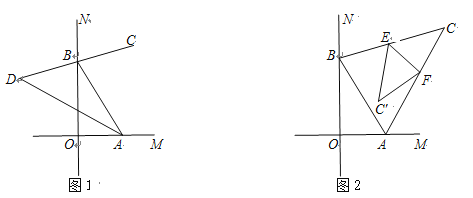
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处。
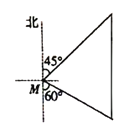
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时)。(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把直线y=-x-1沿x轴向右平移2个单位,所得直线的函数解析式为( )
A. y=-x+1B. y=-x-3C. y=-2x-1D. y=2x-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】46中8年级11班为开展“迎2013年新春”的主题班会活动,派了小林和小明两位同学去学校附近的超市购买钢笔作为奖品,已知该超市的英雄牌钢笔每支8元,派克牌钢笔每支4.8元,他们要购买这两种笔共40支.
(1)如果他们两人一共带了240元,全部用于购买奖品,那么能买这两种笔各多少支?
(2)小林和小明根据主题班会活动的设奖情况,决定所购买的英雄牌钢笔数量要少于派克牌钢笔的数量的![]() ,但又不少于派克牌钢笔的数量的
,但又不少于派克牌钢笔的数量的![]() 。如果他们买了英雄牌钢笔
。如果他们买了英雄牌钢笔![]() 支,买这两种笔共花了
支,买这两种笔共花了![]() 元,
元,
①请写出![]() (元)关于
(元)关于![]() (支)的函数关系式,并求出自变量
(支)的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
②请帮他们计算一下,这两种笔各购买多少支时,所花的钱最少,此时花了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].

(1)、如图①,对△ABC作变换[50°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)、如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)、如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com