
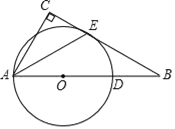
【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
【答案】(1)证明见解析;(2)12.
【解析】试题分析:(1)如图,连接OE.首先证明AC∥OE,推出∠CAE=∠AEO,由OA=OE,推出∠AEO=∠OAE=∠CAE即可证明.
(2)设OE=OA=OD=r,由OE∥AC,得![]() ,即
,即![]() ,解方程即可.
,解方程即可.
试题解析:(1)证明:如图,连接OE.
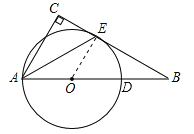
∵BC是⊙O切线,∴OE⊥BC,∴∠OEB=90°,∵∠C=90°,∴∠C=∠OEB=90°,∴AC∥OE,∴∠CAE=∠AEO,∵OA=OE,∴∠AEO=∠OAE=∠CAE,∴AE平分∠CAB;
(2)解:设OE=OA=OD=r,∵OE∥AC,∴ ![]() ,即
,即![]() ,∴r=6(负根已经舍弃),∴BD=OB﹣OD=18﹣6=12.
,∴r=6(负根已经舍弃),∴BD=OB﹣OD=18﹣6=12.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() )0+(-
)0+(-![]() )﹣2
)﹣2
(2)利用乘法公式计算:898×902+4
(3)(3x﹣2y)(﹣3x﹣2y)﹣(4y﹣x)
(4)(a+2b﹣3c)(a﹣2b+3c)
(5)先化简,再求值:[(a+4)2﹣(3a﹣2)a﹣8]+(2a),其中a=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连结
,连结![]() 、
、![]() .
.
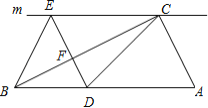
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若点![]() 是
是![]() 中点,当四边形
中点,当四边形![]() 是正方形时,则
是正方形时,则![]() 大小满足什么条件?
大小满足什么条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山是某市民周末休闲爬山的好去处,但总有些市民随手丢垃圾的情况出现.为了美化环境,提高市民的环保意识,某外国语学校某附属学校青年志愿者协会组织50人的青年志愿者团队,在周末前往临某森林公园捡垃圾.已知平均每分钟男生可以捡3件垃圾,女生可以捡2件垃圾,且该团队平均每分钟可以捡130件垃圾.请问该团队的男生和女生各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式.(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
(1)当BG=2,DH=3时,则GH:HF= ,∠AGH= °;
(2)若BG=3,DH=1,求DF、EG的长;
(3)设BG=x,DH=y,若△ABG∽△FDH,求y与x之间的函数关系式,并求出y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2018的坐标是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com