
 ��ͼ��������y=$\frac{1}{4}$x2+bx+c�����ύ�ڵ�A��2��0������B��0��-$\frac{5}{2}$����ֱ��y=kx+$\frac{3}{2}$������A��y�ύ�ڵ�C���������ߵ���һ��������D�㣮
��ͼ��������y=$\frac{1}{4}$x2+bx+c�����ύ�ڵ�A��2��0������B��0��-$\frac{5}{2}$����ֱ��y=kx+$\frac{3}{2}$������A��y�ύ�ڵ�C���������ߵ���һ��������D�㣮���� ��1������A�͵�B��������������ߵĽ���ʽ�����b��c��ֵ��Ȼ�����������ߵĽ���ʽ������A���������ֱ�ߵĽ���ʽ�����k��ֵ���Ӷ������ֱ�ߵĽ���ʽ��
��2���ٽ�y=$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��y=$\frac{3}{4}$x+$\frac{3}{2}$����������õ�D��8��$\frac{15}{2}$����Ȼ������õ�C��0��$\frac{3}{2}$����CE=6�����P������Ϊ��x��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$������M�������ǣ�x��$\frac{3}{4}$x+$\frac{3}{2}$����Ȼ��ɵõ�PM�ij���x�ĺ�����ϵʽ��Ȼ������PM=CE�������x��ֵ���Ӷ��ɵõ���P�����ꣻ
����Rt��CDE�У����ݹ��ɶ�����֪��DC=10�����CDE���ܳ���24����������֤����PMN�ס�CDE���������������ε��ܳ��ȵ������Ʊȿɵõ�m��x�ĺ�����ϵʽ����������䷽�������m�����ֵ��
��� ��1���⣺��y=$\frac{1}{4}$x2+bx+c������A�͵�B��
��$\left\{\begin{array}{l}{1-2b+c=0}\\{c=\frac{5}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=-\frac{5}{2}}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��
��ֱ��y=kx+$\frac{3}{2}$������A��-2��0����
��-2k+$\frac{3}{2}$=0����ã�k=$\frac{3}{4}$��
��ֱ�ߵĽ���ʽΪy=$\frac{3}{4}$x+$\frac{3}{2}$��
��2���ٽ�y=$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��y=$\frac{3}{4}$x+$\frac{3}{2}$���������x=-2��x=8��
��x=8����y=$\frac{3}{4}$x+$\frac{3}{2}$�ã�y=$\frac{15}{2}$��
��D��8��$\frac{15}{2}$����
��x=0����y=$\frac{3}{4}$x+$\frac{3}{2}$�ã�y=$\frac{3}{2}$��
��C��0��$\frac{3}{2}$����
��CE=6��
���P������Ϊ��x��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$������M�������ǣ�x��$\frac{3}{4}$x+$\frac{3}{2}$����
�ߵ�P��ֱ��AD���·���
��PM=��$\frac{3}{4}$x+$\frac{3}{2}$��-��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
���ı���PMECΪƽ���ı��Σ�
��PM=CE��
��-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=6�����x=2��x=4��
��x=2ʱ��y=-3����x=4ʱ��y=-$\frac{3}{2}$��
�൱��P������Ϊ��2��-3����4��-$\frac{3}{2}$��ʱ���ı���PMECΪƽ���ı��Σ�
����Rt��CDE�У�DE=8��CE=6�����ݹ��ɶ�����֪��DC=10��
���CDE���ܳ���24��
��PM��y�ᣬ
���PMN=��DCE��
�֡ߡ�PNM=��DEC=90�㣬
���PMN�ס�CDE��
��$\frac{{l}_{��PMN}}{{l}_{��CDE}}$=$\frac{PM}{DC}$����$\frac{m}{24}$=$\frac{-\frac{1}{4}{x}^{2}+\frac{3}{2}x+4}{10}$��
���������ã�m=-$\frac{3}{5}$x2+$\frac{18}{5}$x+$\frac{48}{5}$��
�䷽�ã�m=-$\frac{3}{5}$��x-3��2+15��
�൱x=3ʱ��m�����ֵ��m�������15��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ�����һ�κ����Ľ���ʽ��ƽ���ı��ε����ʡ����������ε����ʺ��ж����������������ε��ܳ��ȵ������Ʊ��г�m��x�ĺ�����ϵʽ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | |a|+|b| | B�� | |a|-|b| | C�� | |a+b| | D�� | |a-b| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
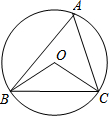 ��ͼ����ABC�ǡ�O���ڽ������Σ�����OB��OC������BAC+��BOC=180�㣬BC=2$\sqrt{3}$cm�����O�İ뾶Ϊ2cm��
��ͼ����ABC�ǡ�O���ڽ������Σ�����OB��OC������BAC+��BOC=180�㣬BC=2$\sqrt{3}$cm�����O�İ뾶Ϊ2cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�Oֱ����C��D�ǻ�AB�����ȷֵ㣬PΪֱ��AB��һ�㣬��AB=12����ͼ����Ӱ���ֵ����Ϊ6�У�
��ͼ��AB�ǡ�Oֱ����C��D�ǻ�AB�����ȷֵ㣬PΪֱ��AB��һ�㣬��AB=12����ͼ����Ӱ���ֵ����Ϊ6�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У�����������y=$\frac{k}{x}$��x��0����ͼ���ھ���OABC�ı�AB�ڵ�D������BC�ڵ�E����BE=2EC�����ı���ODBE�����Ϊ8����k��ֵΪ��������
��ͼ����ƽ��ֱ������ϵ�У�����������y=$\frac{k}{x}$��x��0����ͼ���ھ���OABC�ı�AB�ڵ�D������BC�ڵ�E����BE=2EC�����ı���ODBE�����Ϊ8����k��ֵΪ��������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
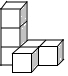 ��ͼ����������ͬ��С�������ɵļ����壬�����ĸ���ͼ�ǣ�������
��ͼ����������ͬ��С�������ɵļ����壬�����ĸ���ͼ�ǣ�������| A�� | 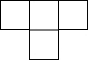 | B�� | 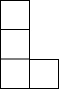 | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com