练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知方程2x-y-5=0，用含有x的代数式表示y的形式为y=2x-5．

    分析 把x看做已知数求出y即可．

    解答 解：方程2x-y-5=0，
    解得：y=2x-5，
    故答案为：y=2x-5

    点评 此题考查了解二元一次方程，解题的关键是将x看做已知数求出y．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”
    【提出问题】三个有理数a、b、c满足abc＞0，求$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值．
    【解决问题】
    解：由题意得：a，b，c三个有理数都为正数或其中一个为正数，另两个为负数．
    ①当a，b，c都是正数，即a＞0，b＞0，c＞0时，
    则：$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=$\frac{a}{a}$+$\frac{b}{b}$+$\frac{c}{c}$=1+1+3；②当a，b，c有一个为正数，另两个为负数时，设a＞0，b＜0，c＜0，
    则：$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=$\frac{a}{a}$+$\frac{-b}{b}$+$\frac{-c}{c}$=1-1-1=-1
    所以：$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值为3或-1．
    【探究】请根据上面的解题思路解答下面的问题：
    （1）三个有理数a，b，c满足abc＜0，求$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值；
    （2）已知|a|=3，|b|=1，且a＜b，求a+b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知反比例函数y=$\frac{k}{x}$的图象与直线y=x+1都过点（-3，n）
    （1）求n，k的值；
    （2）若抛物线y=x2-2mx+m2-m-1的顶点在反比例函数y=$\frac{k}{x}$的图象上，求这条抛物线的顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．分式方程$\frac{2}{x+1}$=$\frac{1}{x-1}$的解为x=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．将5400 000用科学记数法表示为5.4×106．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

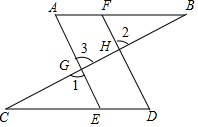    2．请把以下证明过程补充完整，并在下面的括号内填上推理理由：
    已知：如图，∠1=∠2，∠A=∠D．
    求证：∠B=∠C
    证明：∵∠1=∠2，（已知）
    又：∵∠1=∠3，对顶角相等
    ∴∠2=∠3，（等量代换）
    ∴AE∥FD同位角相等，两直线平行
    ∴∠A=∠BFD两直线平行，同位角相等
    ∵∠A=∠D（已知）
    ∴∠D=∠BFD（等量代换）
    ∴AB∥CD内错角相等，两直线平行
    ∴∠B=∠C两直线平行，内错角相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

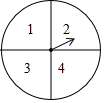    9．元旦期间，某商场设置了如图所示的幸运转盘，转盘分成4个大小相同的扇形，分别标有数学1，2，3，4，指针的位置固定，转盘可以自由转动，当转动的转盘停止后，其中的某个扇形会停在指针所指的位置（指针指向两个扇形的交线时，当作右边的扇形）．商场规定：凡是参加抽奖的顾客均可转动转盘两次，如果两次转动中指针指缶扇形上的数字之和为8是一等奖，数字之和为7是二等奖，数字之和为6是三等奖，标号之和为其他数字则获得一份纪念品，请分别求出顾客抽中一、二、三等奖的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

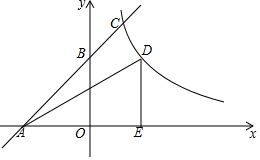    6．在平面直角坐标系内，点O为坐标原点，直线y=x+4交x轴于点A，交y轴于点B，点C（2，m）在直线y=x+4上，反比例函数
    y=$\frac{n}{x}$经过点C．
    （1）求m，n的值；
    （2）点D在反比例函数y=$\frac{n}{x}$的图象上，过点D作X轴的垂线，点E为垂足，若OE=3，连接AD，求tan∠DAE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如下数表是由从l开始的连续自然数组成，观察规律并完成各题的解答．

    （l）表中第8行的最后一个数是64，它是自然数8的平方，第8行共有15个数；
    （2）用含n的代数式表示：第n行的第一个数是（n-1）2+1，最后一个数是n2，第n行共有2n-1个数．

    查看答案和解析>>

    同步练习册答案