
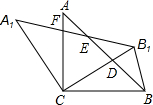
 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F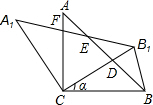 (1)证明:∵AC=BC,
(1)证明:∵AC=BC,
|
| 180°-α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| α |
| 2 |
| α |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
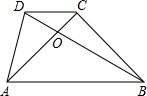 在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )
在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )| A、4:9 | B、6:9 |
| C、8:9 | D、10:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
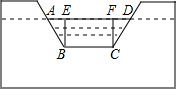 如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.
如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.查看答案和解析>>
科目:初中数学 来源: 题型:
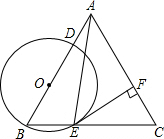 如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.查看答案和解析>>
科目:初中数学 来源: 题型:
 一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com