
【题目】如图,点E是正方形ABCD内的一点,将△BEC绕点C顺时针旋转至△DFC.
(1)请问最小旋转度数为多少?
(2)指出图中的全等图形以及它们的对应角?
(3)若∠EBC=30°,∠BCE=80°,求∠F的度数.

【答案】(1)90°;(2)△BCE≌△DCF,对应角为:∠CBE与∠CDF,∠BCE与∠DCF,∠BEC与∠DFC;(3)70°.
【解析】试题分析:(1)根据正方形的性质得CB=CA,∠BCA=90°,然后根据旋转的定义得到△BEC绕点C顺时针旋转得到△DFC的最小旋转度数为90°;
(2)根据旋转的性质得△BCE≌△DCF,再根据全等的性质写出对应角;
(3)先根据三角形内角和定理计算出∠BEC=70°,然后根据(2)中的结论求解.
试题解析:(1)∵四边形ABCD为正方形,
∴CB=CA,∠BCA=90°,
∴△BEC绕点C顺时针旋转90°可得到△DFC,
∴最小旋转度数为90°;
(2)△BCE≌△DCF,对应角为:∠CBE与∠CDF,∠BCE与∠DCF,∠BEC与∠DFC;
(3)∵∠EBC=30°,∠BCE=80°,
∴∠BEC=180°-30°-80°=70°,
∴∠F=∠BEC=70°.


科目:初中数学 来源: 题型:
【题目】如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米。

A. 80 B. 50![]() C. 100
C. 100![]() D. 100
D. 100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示-3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.
(2)如果|x+1|=3,那么x= ;
(3)若|a-3|=2,|b+2|=1,且数a、b在数轴上表示的数分别是点A、点B,则A、B 两点间的最大距离是 .
(4)若数轴上表示a的点位于-4与2之间,则|a+4|+|a-2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由一些火柴棒搭成的图案:
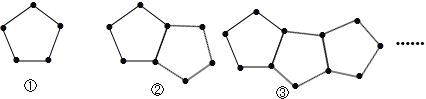
(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com