
分析 (1)过点B作BE⊥AC于点E,在直角三角形AEB中,利用锐角三角函数定义求出AE的长,在直角三角形CEB中,利用锐角三角函数定义求出BE与CE的长;
(2)由AE+CE求出AC的长,即可求出CD的长.
解答 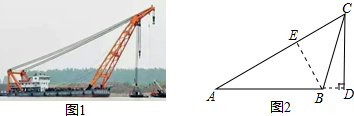 解:(1)过点B作BE⊥AC于点E,
解:(1)过点B作BE⊥AC于点E,
在Rt△AEB中,AB=100m,sinA=$\frac{1}{2}$,BE=ABsinA=100×$\frac{1}{2}$=50m,cosA=$\frac{AE}{AB}$,
∴AE=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$m,
在Rt△CEB中,∠ACB=∠CBD-∠A=75°-30°=45°,
∴BE=CE=30m,
(2)AC=AE+CE=(50+50$\sqrt{3}$)m,
在Rt△ADC中,sinA=$\frac{CD}{AC}$,
则CD=(50+50$\sqrt{3}$)×$\frac{1}{2}$=(25+25$\sqrt{3}$)m.
点评 此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是63$\frac{4}{7}$分钟.
小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是63$\frac{4}{7}$分钟.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有10个边长为1的正方形,排列形式如下左图.请在左图中把它们分割,使之拼接成一个大正方形,并把分割后的图形画在右图的正方形网格中.(正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,要求以格点为顶点画大正方形)
有10个边长为1的正方形,排列形式如下左图.请在左图中把它们分割,使之拼接成一个大正方形,并把分割后的图形画在右图的正方形网格中.(正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,要求以格点为顶点画大正方形)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x+3 | B. | y=2x-3 | C. | x=$\frac{3-y}{2}$ | D. | x=$\frac{3+y}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 物体质量x/千克 0 1 2 3 4 5… |
| 弹簧长度y/厘米 10 10.5 11 11.5 12 12.5… |
| A. | x与y都是变量,其中x是自变量,y是因变量 | |
| B. | 弹簧不挂重物时的长度为0厘米 | |
| C. | 在弹簧范围内,所挂物体质量为7千克时,弹簧长度为13.5厘米 | |
| D. | 在弹簧范围内,所挂物体质量每增加1千克弹簧长度增加0.5厘米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com