
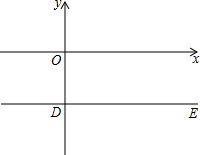
 已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.
已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.分析 (1)在y=2x+2b中分别令y=0和y=-2可分别求得相应的x的值,则可求得A、B两点的坐标;
(2)由A、B、D的坐标可用b表示出AB和BD的长,由条件可得AB=BD,可得到关于b的方程,可求得b的值;
(3)由条件可证明△CBD∽△CAO,利用相似三角形的性质可求得CD和CO的关系,分点C在点D下方和上方两种情况可分别求得OC的长,则可求得b的值.
解答 解:
(1)当y=0时,2x+2b=0,x=-b,
当y=-2时,2x+2b=-2,x=-b-1,
∴A(-b,0),B(-b-1,-2);
(2)∵A(-b,0),B(-b-1,-2),D(0,-2);
∴AB=$\sqrt{(-b-1+b)^{2}+(-2)^{2}}$=$\sqrt{5}$,BD=|-b-1|,
∵△ABD是以AD为底边的等腰三角形,
∴AB=BD,即|-b-1|=$\sqrt{5}$,
解得${b_1}=\sqrt{5}-1$,${b_2}=-\sqrt{5}-1$;
(3)∵DE∥x轴,
∴△CBD∽△CAO,
∴$\frac{S△CDB}{S△CAO}={({\frac{CD}{CO}})^2}=\frac{1}{4}$,
∴$\frac{CD}{CO}=\frac{1}{2}$,
①如图1,当点C在点D下方时,
∴CO=2OD=4,
∴C(0,-4),
∴b=-2;
②如图2,当点C在点D上方时,
∴$CO=\frac{2}{3}OD=\frac{4}{3}$,
∴$C({0,-\frac{4}{3}})$,
∴$b=-\frac{2}{3}$;
综上可知b的值为-2或-$\frac{2}{3}$.
点评 本题为一次函数的综合应用,涉及勾股定理、等腰三角形的性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(1)注意函数图象的交点坐标的求法,在(2)中用b分别表示出AB和BD的长是解题的关键,在(2)中利用相似三角形的性质求得CD和CO的关系是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
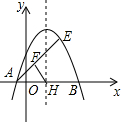 如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).
如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
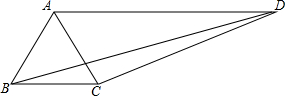 在四边形ABCD中,连接对角线AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,则BD=3$\sqrt{13}$.
在四边形ABCD中,连接对角线AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,则BD=3$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
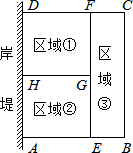 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com