
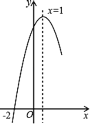
【题目】抛物线![]() 经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①![]() ;
;
②![]() >
>![]() ;
;
③若n>m>0,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值;
时的函数值;
④点(![]() ,0)一定在此抛物线上.
,0)一定在此抛物线上.
其中正确结论的个数是( )
A.4个B.3个
C.2个D.1个
【答案】C
【解析】
利由抛物线的对称轴为x=1可对①进行判断;利用抛物线![]() 经过点(﹣2,0),代入解析式则可对②进行判断;由抛物线的对称性和二次函数的性质可对③进行判断;抛物线的对称性得出点(-2,0)的对称点是(4,0),由c=-8a 即可得出
经过点(﹣2,0),代入解析式则可对②进行判断;由抛物线的对称性和二次函数的性质可对③进行判断;抛物线的对称性得出点(-2,0)的对称点是(4,0),由c=-8a 即可得出![]() ,则可对④进行判断.
,则可对④进行判断.
∵抛物线的对称轴为![]() ,
,
∴b=-2a,
故①错误;
∵抛物线y=ax2+bx+c经过点(-2,0),
∴4a-2b+c=0,
故②错误;
∵抛物线开口向下,对称轴为直线x=1,
∴横坐标是1-n的点的对称点的横坐标为1+n,
∵n>m>0,
∴1+n>1+m,
∴x=1+m时的函数值小于x=1-n时的函数值,故③正确;
∵b=-2a,
∴抛物线为y=ax2-2ax+c,
∵抛物线y=ax2+bx+c经过点(-2,0),
∴4a+4a+c=0,即8a+c=0,
∴c=-8a,
∴![]() ,
,
∵点(-2,0)的对称点是(4,0),
∴点(![]() ,0)一定在此抛物线上,故④正确,
,0)一定在此抛物线上,故④正确,
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
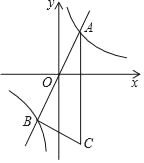
【题目】如图,反比例函数的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°
(1)求反比例函数的解析式及点B的坐标;
(2)求tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点A(3,1)与点B(0,4).
经过点A(3,1)与点B(0,4).

(1)求该抛物线的解析式及顶点坐标;
(2)在第三象限内的抛物线上有一点P,使得PA⊥AB,求点P的坐标;
(3)若点C(![]() ,
,![]() )在该抛物线上,当
)在该抛物线上,当![]() ≤
≤![]() ≤3时,1≤
≤3时,1≤![]() ≤5,请确定
≤5,请确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=8,BC=6,点E,F分别为AB,AD边上任意一点,现将△AEF沿直线EF对折,点A对应点为点G.
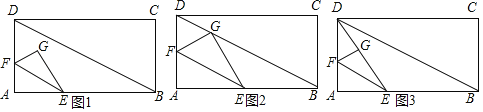
(1)如图2,当EF∥BD,且点G落在对角线BD上时,求DG的长;
(2)如图3,连接DG,当EF∥BD且△DFG是直角三角形时,求AE的值;
(3)当AE=2AF时,FG的延长线交△BCD的边于点H,是否存在一点H,使得以E,H,G为顶点的三角形与△AEF相似,若存在,请求出AE的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
A公司方案:无纺布的价格均为每吨1.95万元![]() ;
;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
设甲厂在同一公司一次购买无纺布的数量为x吨(x>0).
(Ⅰ)根据题意,填写下表:
一次购买数量(吨) | 10 | 20 | 35 | … |
A公司花费(万元) | 39 | … | ||
B公司花费(万元) | 40 | … |
(Ⅱ) 设在A公司花费![]() 万元,在B公司花费
万元,在B公司花费![]() 万元,分别求
万元,分别求![]() 、
、![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)如果甲厂所需购买的无纺布是50吨,试通过计算说明选择哪家公司费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
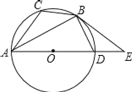
⑴求证:BE是⊙O的切线;
⑵若BC=![]() ,AC=5,求圆的直径AD的长.
,AC=5,求圆的直径AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 和
和![]() 上,沿
上,沿![]() 折叠四边形
折叠四边形![]() ,使点
,使点![]() 、
、![]() 分别落在
分别落在![]() 、
、![]() 处,得四边形
处,得四边形![]() ,点
,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;
;
③![]() ;④若点
;④若点![]() 是
是![]() 的中点,则
的中点,则![]() ,其中,正确结论的序号是_______.(把所有正确结论的序号都在填在横线上)
,其中,正确结论的序号是_______.(把所有正确结论的序号都在填在横线上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com